Deep Neural Networks
CouseraのDeepLearningのコース. コース1の最終週分です.
Deep L-layer neural network
2層や3層の浅いモデルでは,性能的に限界があるので,より高い性能を求めて深いニューラルネットワークが活用されるようになった.
浅いニューラルネットワークでは使っていなかったが,新たな記法としてL(総ノード数)を今後は使っていく.
Forward Propagation in a Deep Network
深いネットワークにおける順伝播を定式化する. まず,単純に1サンプルに対する順伝播を考えると,図1のように定式化できる.
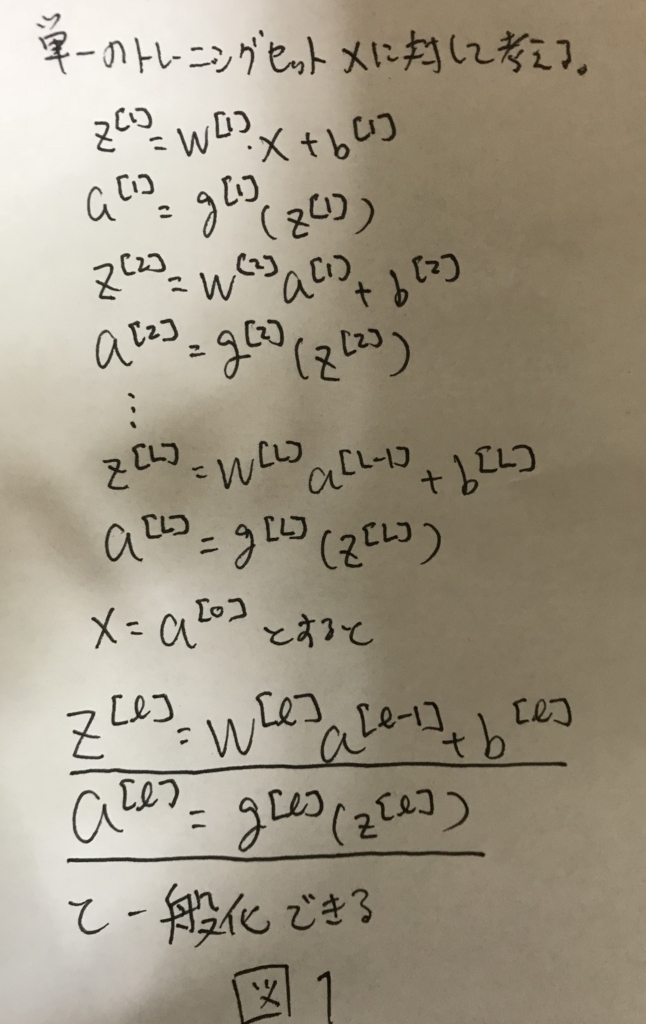
これをmサンプルに拡張し,ベクトル化すると,図2のように表せる.
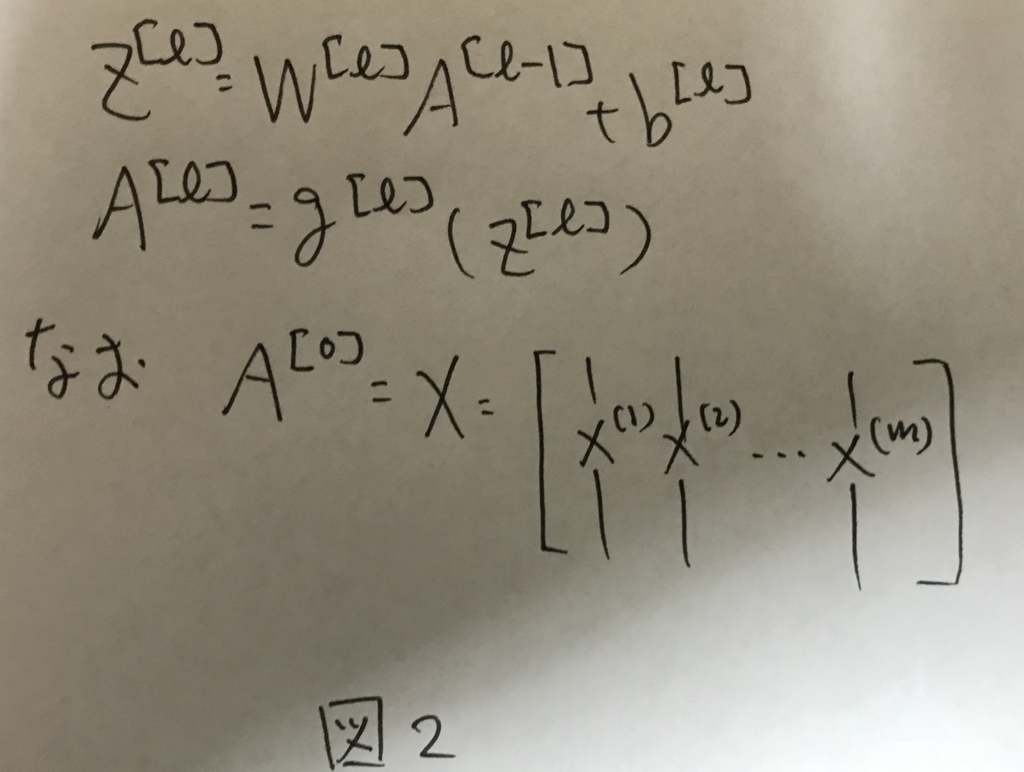
これがDeepNetworkにおける順伝播の式となる.
Getting your matrix dimensions right
各実装を行なっていく上で,各行列のサイズを意識してコーディングしていくとバグが減らせる.そこで,この章では各行列のサイズを明らかにする.
図3のようなネットワークを考える.
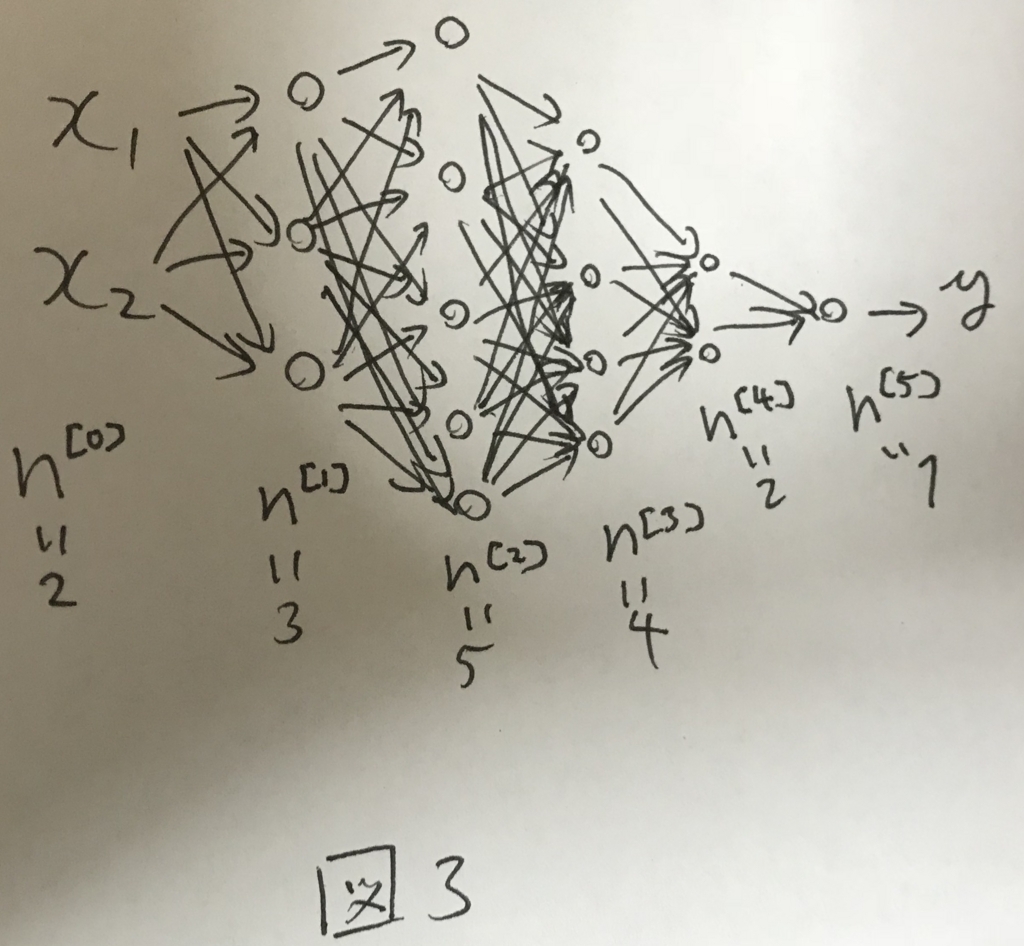
この時,1サンプルのみを考えると各行列のサイズは図4のようになる.
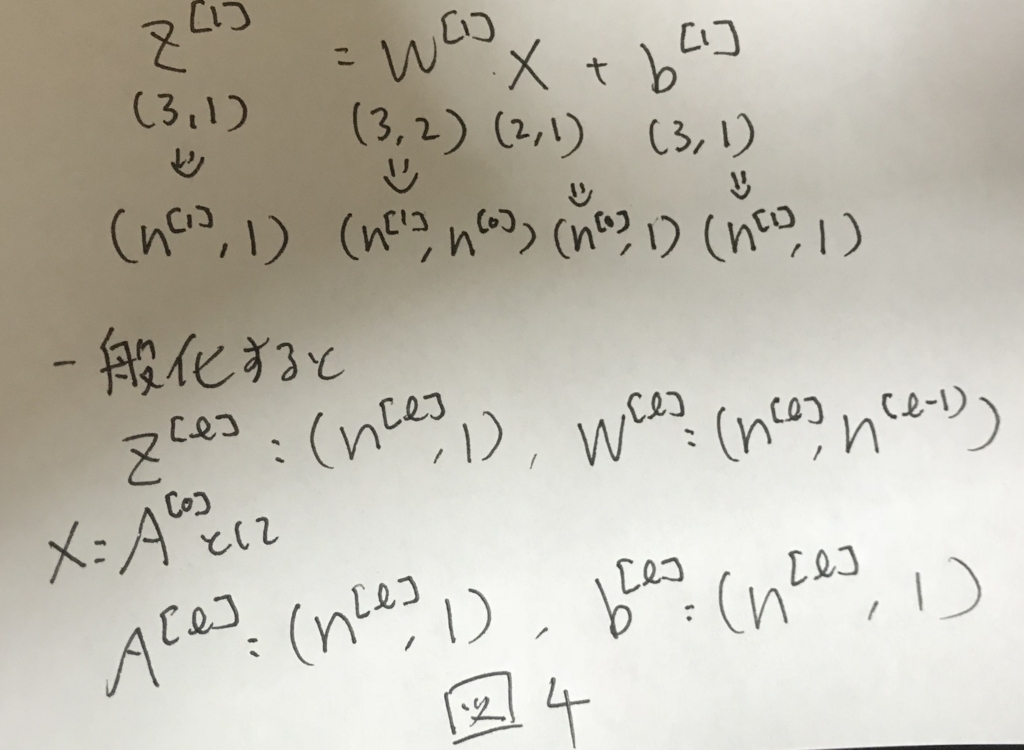
さらに,これをmサンプルに拡張すると図5のようになる.
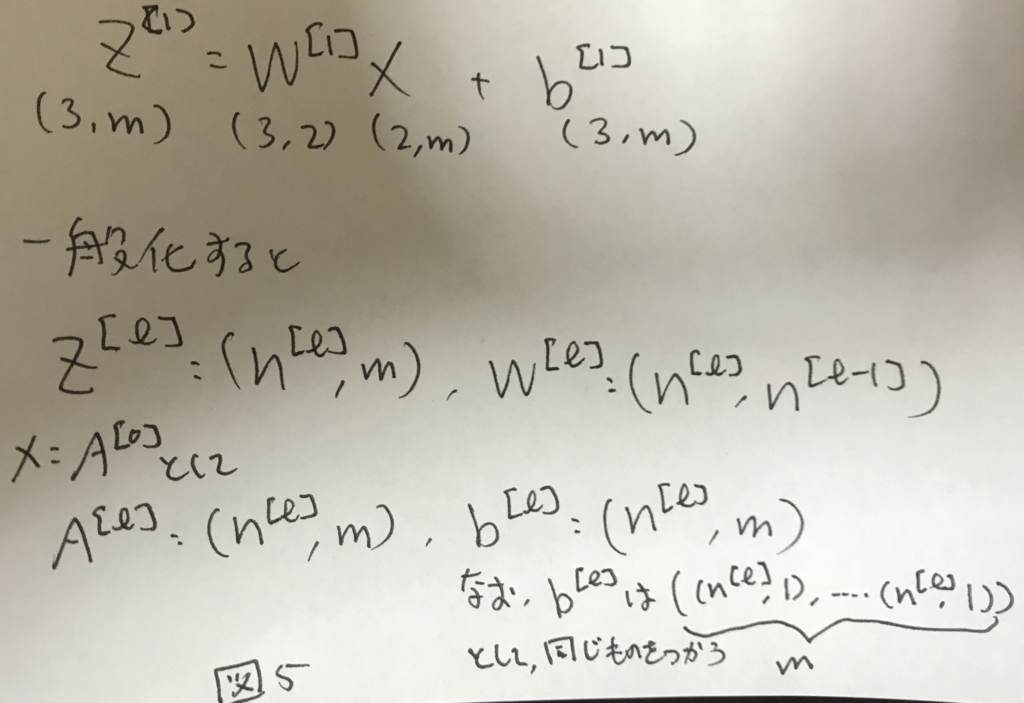
なお,b^[l]については,サンプルごとに異なるものを用いるのではなく全てのサンプルに対して同様のものを使い回すこと.
Why deep representations?
深いネットワークにすると,より複雑なことができるようになる.
これをイメージ的に説明する.
例えば顔画像認識のネットワークについて,はじめの方の層は例えば画像のエッジや境界線を検出するような単純なものを検出するために働く. これが,中段の層になると.下位の層の単純なものを組み合わせて例えば目や鼻を検出するようなことができるようになる.
さらに深い層になると,目や鼻を組み合わせて様々な顔のパターンを検出できるようになることで,顔の画像認識が高い精度で実現できる.
このように,下位の層で抽出したシンプルな特徴を組み合わせて,深い層では複雑なパターンの認識ができるようになる.
これによって,より例えば画像認識であればより精度が高まるなど,複雑なことができるようになる.
画像の例だけでなく,例えば音声認識では,下位の層は音の上がり下がりなどの簡易的な特徴を捉えるが,深い層になるについれて音素を識別し,さらに深い層ではそれを組み合わせて単語を識別したりできるようになる.
これが,深い層でより複雑なことができるようになることについての直感的な説明である.
BUilding blocks of deep neural networks
これまでの内容を一枚の図でまとめると図6のようになる.
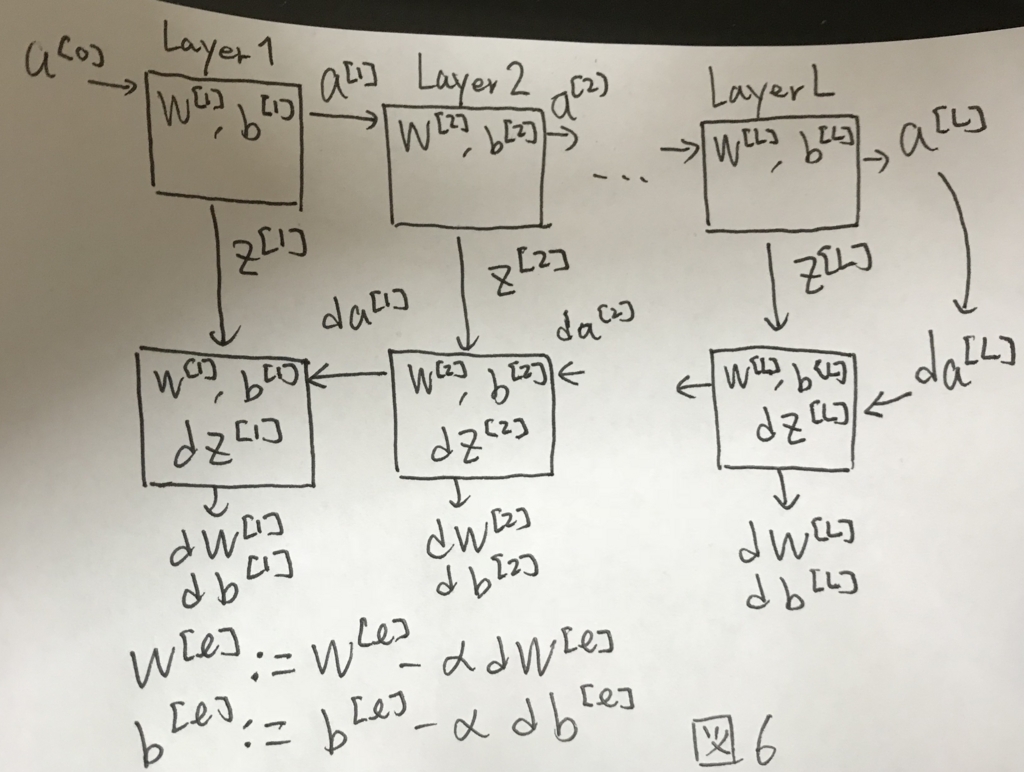
ここには深いネットワークにトレーニングデータが入力され,推定値が計算され,その誤差を持ってネットワークが学習するといった1stepが示されている.
これを何度も繰り返して,モデルを学習する.
Forward and Backward Propagation
図6で行う具体的な計算を図7にまとめる.

Parameters vs Hyperparameters
ニューラルネットのパラメータはこれまで見て来た通り,Wやbがある, これらとは別に,アルゴリズムに与えないといけないHyperParameterがいくつかある. 以下にその一覧を示す.
- Learning rate α
- イテレーション数(学習回数)
- 隠れ層のレイヤー数(L)
- 各レイヤーのユニット数(n^[1],...,n^[L])
- 活性化関数としてどれを選ぶか
これらのhyperparameterはアプリケーション毎に調整する必要がある. コスト関数の収束度合いからLearning rateを調整したり,レイヤ数を調整したり,CrossValidationの結果からも様々なHyperparameterを調整する必要がある.
What dose this have to do with the brain?
ニューラルネットの説明として,よく使われる脳に似ているという表現は,ニューラルネットの研究の進歩に伴って,陳腐化してきている.
シナプスとニューロンの関係性はわかりやすい類似性がある一方で,その学習過程などについては,脳の学習機構も同様に逆伝播が活用されているのかそうではないのかなど,まだ解明されていない.
CNNの文脈では脳の構造から着想を得た部分が大きいが,一方で通常のニューラルネットについては脳との関連性はあまりなくなって来ているのが現状.
キャッチーでわかりやすいが,厳密性はあまりなくなっているのが現状.
Shallow neural networks
CouseraのDeep Learningコースの第1コースの3週目
Neural Networks Overview
ニューラルネットワークの大枠の説明. 以降の章で話されることが端的に出てくる.
Neural Network Representation
前回学んだロジスティック回帰のノードを複数結合させたようなものをニューラルネットワークと呼ぶ(図1).
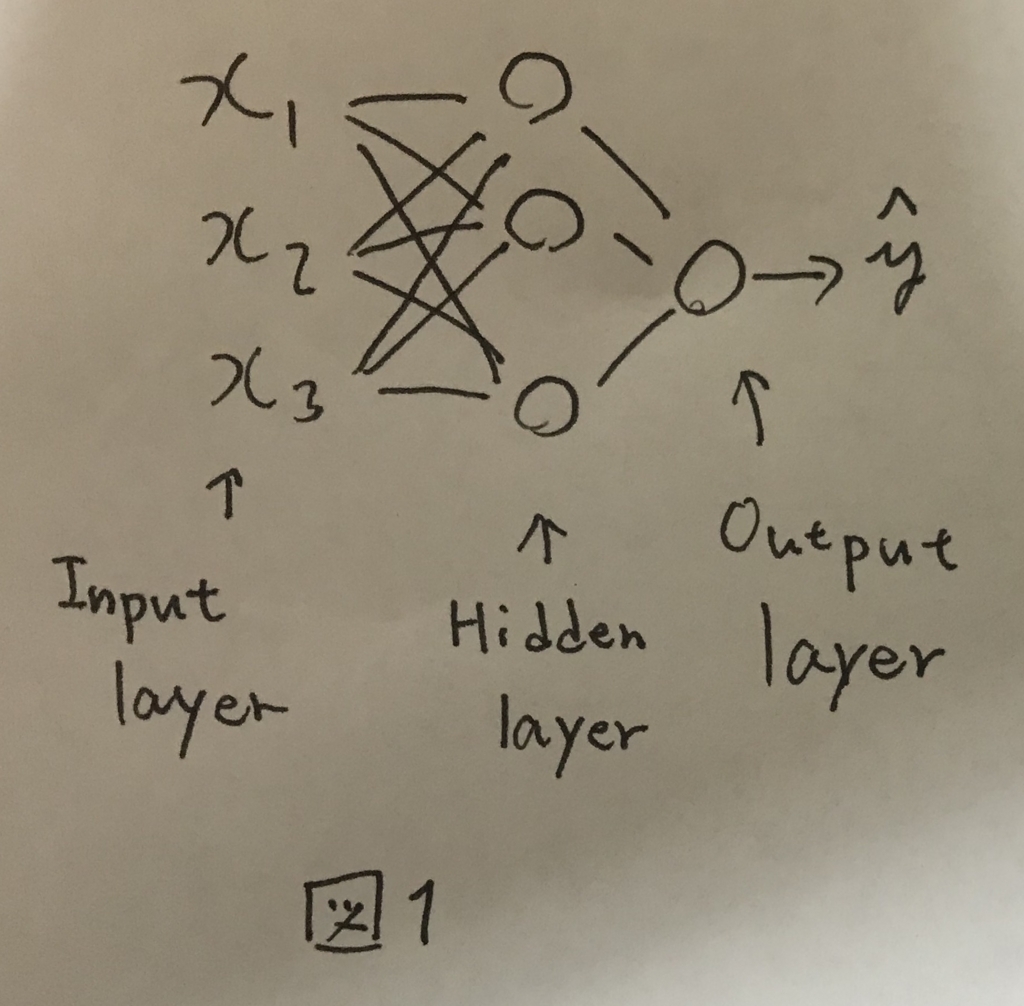
入力のノード群をInput Layer,出力のノードをOutput Layerと呼び,真ん中の層をHidden Layerと呼ぶ.
トレーニングセットにはInputLayerとOutputLayerのデータのみが含まれ,HiddenLayerの情報は含まれない.そのためHiddenLayer(隠れ層)という表現で呼ばれる.
図1のニューラルネットワークは2層のニューラルネットワークと呼ばれ,慣習的にInputLayerはカウントしない.
各レイヤーの出力する値は図2のようにそれぞれa^[i]で表される.
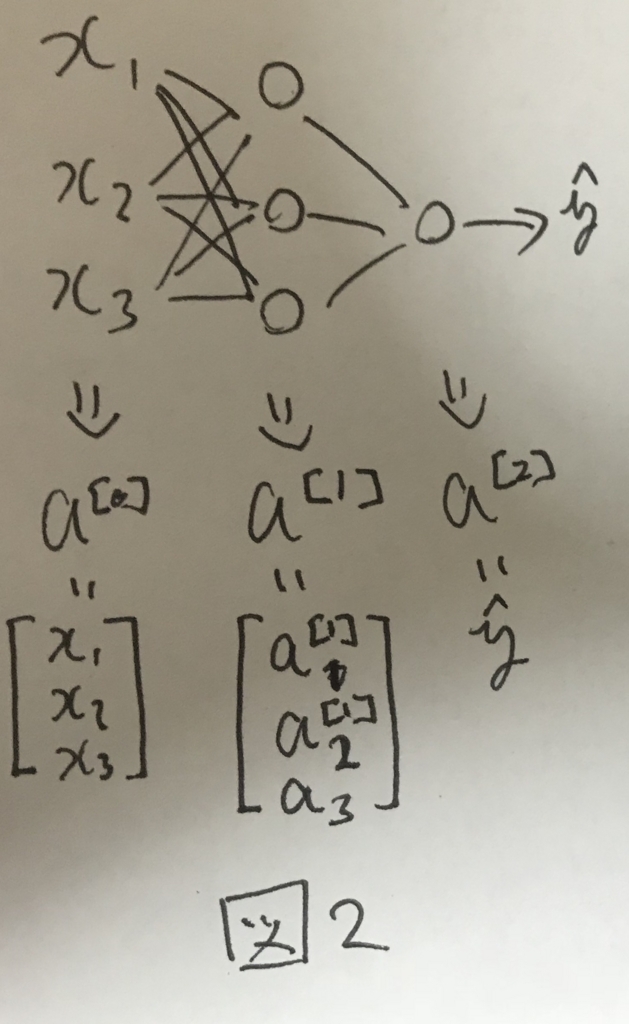
Computing a Neural Network's Output
各ノードは自身へのインプットと重みの計算と活性化関数の処理を行う. 活性化関数は後述するが,ロジスティック回帰のSigmoid関数をイメージすればよい.
図3に第一層で行われる処理のイメージを示す.
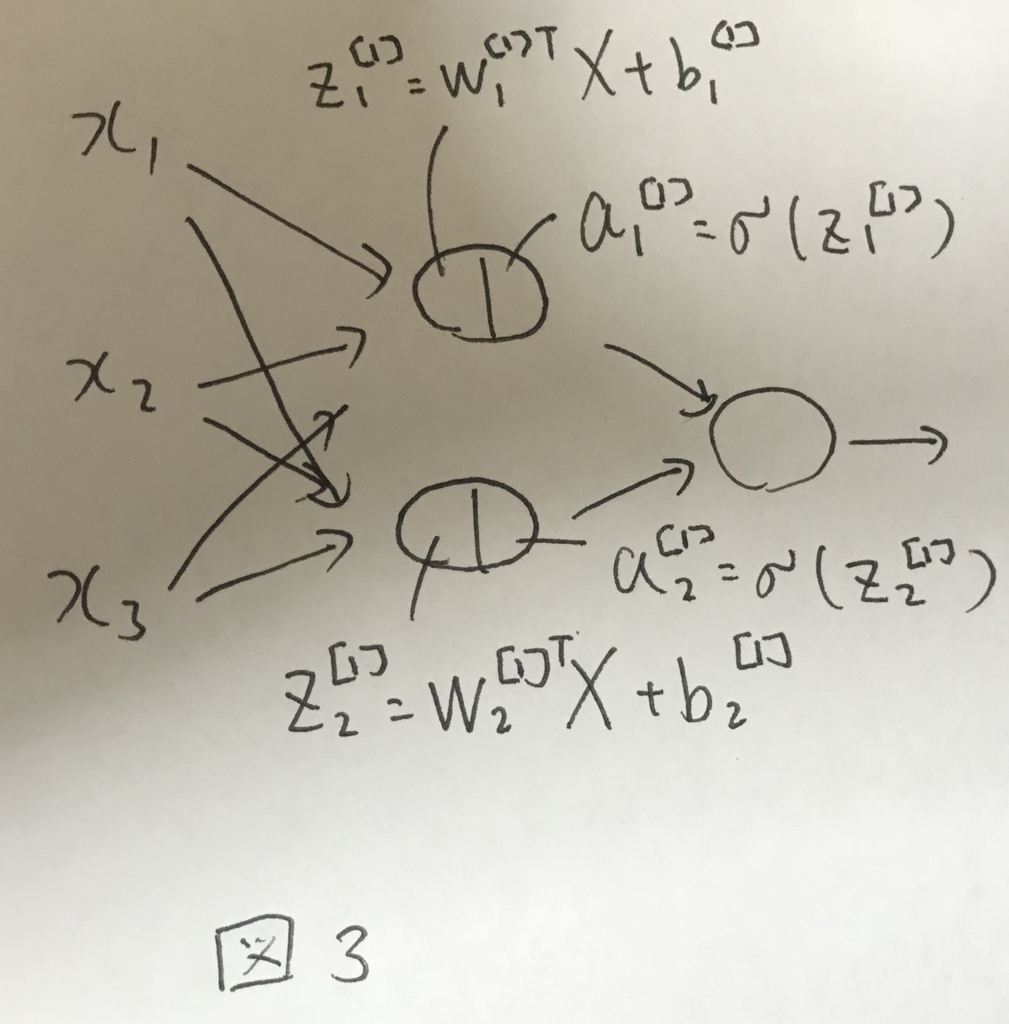
前の章でもあったように,ニューラルネットワークを実装する上では,ベクトル化が重要になる.
図3の処理を2層目にも適用し,ベクトル化すると図4のように表せる.
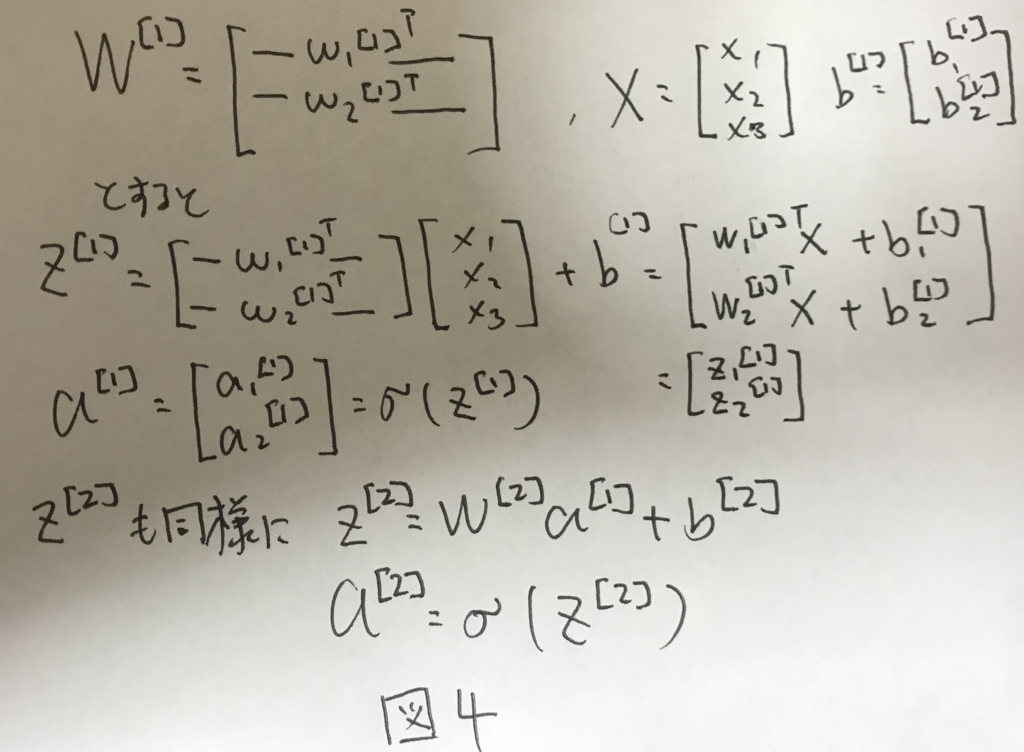
Vectorizeing across multiple examples
図4をさらに,トレーニングサンプルについて拡張してベクトル化すると図5のように表せる.

Explanation for Vectorized Implementation
これまでの振り返りなので割愛.
Activation functions
活性化関数についてのお話. これまではシグモイド関数だった部分について,ほかの選択肢として図6に示す3つがあげられた.
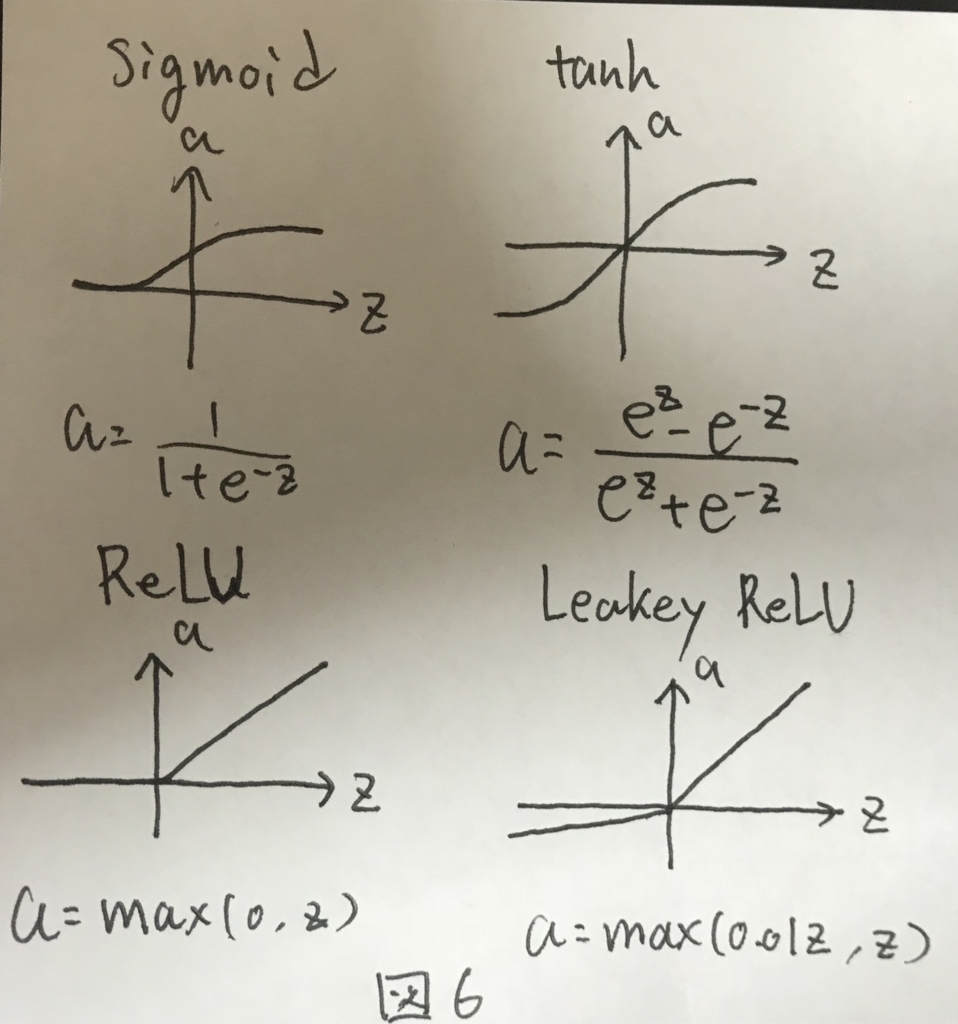
シグモイド関数は限られた用途のニューラルネットワークでしか用いられない. 代わりにtanhもしくはReLU関数が用いられる.
特にReLU関数はおすすめで,とある問題を解決することができる. とある問題とは,ニューラルネットワークにて最急勾配法を行う際に,活性化関数の微分した形が必要になる際に,引数Zの値が大きくなりすぎることで発生する問題であり,これが発生すると学習の効率が著しく下がる.
引数Zの値が大きくなると,tanhやsigmoid関数の場合,勾配がほぼ0となり,その結果として学習が全く進まないからである.
ReLU関数はZがどれだけ大きくなったとしても勾配は常に一定であり,上記の問題が発生しないという特性がある.そのため,ReLU関数は活性化関数としてよく用いられる.
なお,これまで見てきた4つの関数はいずれも非線形な関数であり,線形な関数は基本的に活性化関数として向かない.その理由は次の章で説明する.
Why do you need non-linear activation functions
図5において,A^[i]を求める際に用いる関数が例えばf(z)=zだったとする(線形関数). すると,図7のように,最終的に1層のニューラルネットワークとして表す値の組み合わせを見つけることができる.
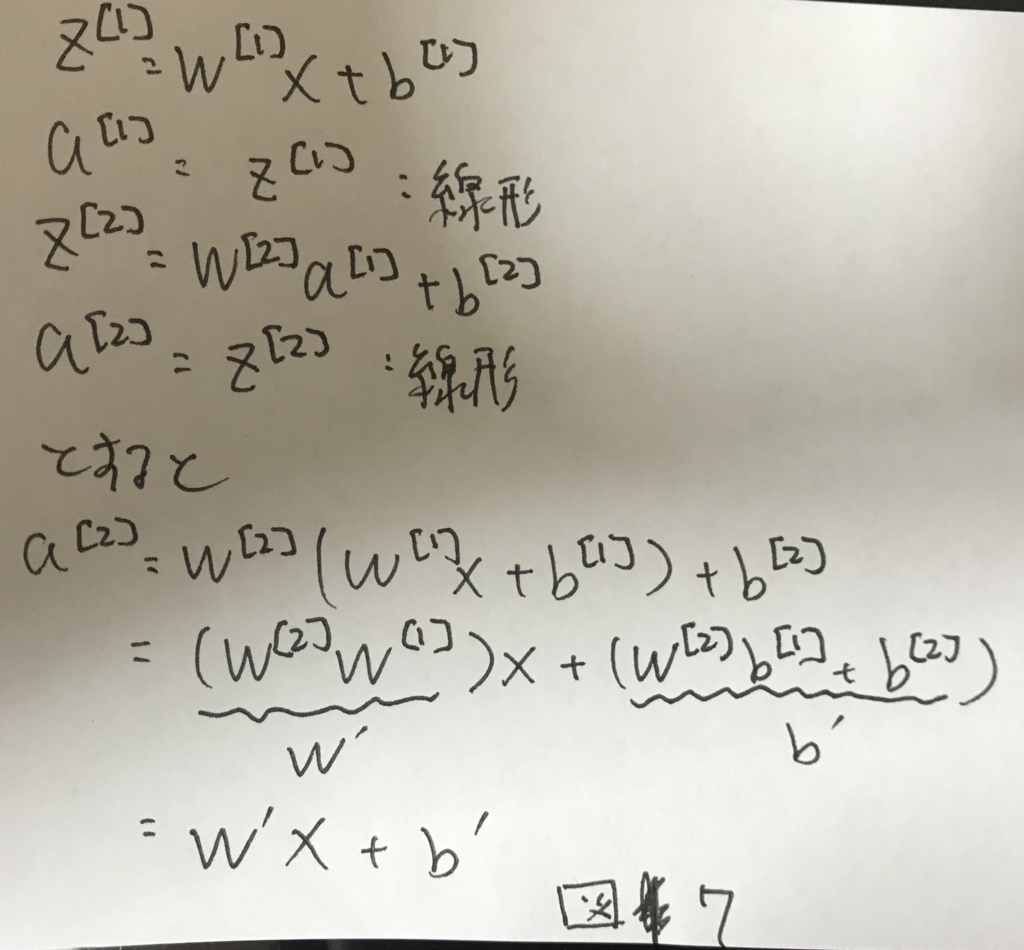
これは如何に多段にしても変わることはなく,何層にしたところで,線形関数を用いている以上は最終的には1ノードで表すことができる. そのため,表現力の高いモデルにはならず,多段にする意味がない.
これを避けるために非線形な関数を活性化関数として採用しなくてはいけない.
Derivatives of activation functions
次の章で詳細は述べるが,最急勾配法を行うためには活性化関数の微分形が必要になる. 各活性化関数の微分形を図8に示す.

Gradient descent for Neural Networks
計算グラフから,ニューラルネットワークでの最急勾配法を定式化する. まず,解きたい問題のアルゴリズムを図9に示す.

これを計算グラフを使って表すと図10のように定式化できる.
なお,np.sum(A, axis=1, keepdims=True)は,Aを縦方向にsumして,得られる解の形を(n,1)とするためのもの.keepdimsがないと,pythonの仕様から,(n,)という形状で返って来てしまうので扱いにくくなる.型を揃えるためのおまじないみたいなもの.

ここまで,図5では2層ニューラルネットの順伝播による推定を,図10では2層ニューラルネットの逆伝播による学習を定式化した.
これで,2層のニューラルネットの学習並びに推定において必要なことはほぼ出揃った.
次章では細かいことだが,重要な各パラメータの初期化について述べる.
Random Initialization
2層ニューラルネットワークではパラメータがw1,b1,w2,b2と4つあった. このうち,b1,b2については初期化時に考慮しなければならない特別な問題はないので,一般的には全て0で初期化される.
一方で,W1,W2については初期化時にそれぞれの要素をランダムで小さい値で初期化する必要がある.
初期化時にランダムな値ではなく,全て0で初期化すると,各レイヤーにおいて,ノード同士の出力の値が等しくなる.順伝播を繰り返し,誤差を計算して逆伝播する際に,出力が各レイヤー内部のノード同士で等しかったので,等しい値で学習が行なわれる. どれだけ学習を繰り返したところで,各レイヤー間の各ノードの値同士が等しい状況は変わらず,学習がうまくいかない. この問題を対称性の破れという.
これを避けるために,それぞれノードの初期値はランダムで初期化してあげる必要がある.
さらに,初期化の値を大きくした場合,活性化関数としてシグモイド関数やtanh関数を用いた場合,微分形の値がほぼ0になるため,学習が進まない.
そのため,各初期値は十分小さい値でランダムに初期化する必要がある.
Neural Networks Basics
CouseraのDeep Learningのコースのお勉強メモpart2
Binary Classification
ニューラルネットワークの説明の前に,先ずは簡単な導入としてLogistic回帰を説明する.
ロジスティック回帰とは,Yes/Noを予測するアルゴリズム. 例えば写真に猫が写っているという問いに対するYes/Noを予測する.
ロジスティック回帰のinputとしては,画像をそのまま使うのではなく,画像のRGBの各ピクセルを1列に並べ替えたベクトルを用いる(図1).

このベクトルの要素数をnxと呼ぶ.
他にも,数学的な記法として図2のようなものがある.今後はこれを使って行く.

Logistic Regression
このアルゴリズムでは,inputを受け取って,inputが問いに対してYesとなる確率(0~1の範囲)を計算する. その際のパラメータとしてwとbの2つがある.なお,wはベクトルで,bは実数.
計算方法は図3の通りで,ベクトル同士の内積にbを加えてシグモイド関数をかけたら完成.

シグモイド関数は図に示す通り,0~1の値をとる関数.
y^が正しい値になるように,パラメータのwとbを学習し,そのパラメータを用いて,Yesとなる確率を計算する.
Logistic Regression Cost Function
ロジスティック回帰では,できるだけy予測値とy(実測値)を近づけたい.
予測値と実測値の近さを評価する関数を損失関数とよび,図4のように表現する. ややこしい数式っぽく見えるが,これはこのあと出てくる最急勾配方をうまく動かすために必要な工夫なので,詳細は割愛.

全ての教師データ(トレーニングセット)に対して平均的により良いパラメータを求めたいので,全てのトレーニングセットについてどれだけ正しく予測できたかという指標として,Cost関数を図4のように定義した.
これを小さくするためのwとbを探すことが,学習である.
Gradient Descent
最急勾配法についての説明.
Logistic Regression Cost Functionにて,なんだかややこしい損失関数を定義していたが,そのお陰でCost関数が下に凸な形状になる(図5).

このCost関数を一番小さくするwが求めたい.図中のw_{min}がそれ. これを行うための簡単な方法として最急勾配法がある.
アルゴリズムは以下の通り.
- 適当な値にwを初期化する
- J(w)の値が小さくなる方向にwを少しだけ更新する
- 収束するまで繰り返す
ここで更新する式は図6の通り.

なぜこれを繰り返すことでw_{min}に近づくかを以下で説明する.
まず,図7のようにw0としてwが初期化される.

更新式にある微分を計算すると,w0の地点でのJ(w)の傾きがわかる.
w0+であれば微分結果は正の値になるし,w0-であれば負の値になる. これに学習率を掛け合わせて1stepの歩幅が決まり,更新式の通りに更新される.
w0+の場合は微分結果が正であり,aもまた正なので,wは小さくなる方向に更新される. これを繰り返すとw_{min}に近づく.
逆にw0-の場合は微分結果が負になり,aは正なので,wは大きくなる方向に更新される. これを繰り返すことでw_{min}に近く.
最急勾配法はこんな感じでCost関数を最小化するwを見つけることができる.
Derivatives
微分の簡単な説明なので割愛
More Derivatives Excamples
微分の簡単な説明なので割愛
Computaion Graph
順伝播と逆伝播の説明に欠かせない,計算グラフについて説明する. 先ずは簡単な例としてJ(a,b,c)= 3 * (a + b * c)を計算グラフで表すと図8のようになる.

a,b,cそれぞれに値を入れて,順順に値を伝播させ,Jを求める作業を順伝播と呼ぶ.
Derivation with a Computation Graph
計算グラフを用いて簡単に微分を求めることができる.その方法を逆伝播と呼ぶ.
順伝播とは逆に,最終結果から1つずつ微分を求めて行くと図9のように,a,b,cそれぞれによる微分を簡単に求めることができる.

この知見を最急勾配法で必要な微分計算に用いる.
Logstic Regression Gradient Desent
計算すると,図10のようになる.

Gradient Desent on m Example
上記はあくまで1サンプルに対して成り立つ方法だった. これをm個のトレーニングセットについて適用すると図11のようになる.

Python and Vectorization
実際にコーディングする際には,最適化と並列実行をサポートするために,明示的なFor文を極力書かずに実装する必要がある.このテクニックをベクトル化とよぶ.
これによって実行速度がかなり変わってくる.簡単な例であっても300倍ほどの違いにもつながるので,とても大事なテクニック.
ベクトル化することで図11のFor文があってわかりにくかった記載が図12までシンプルに記載でき,実行速度の面でもかなり有利になる.

Neural Networks and Deep Learning introduction
CouseraのDeep Learningのコースを以前受けていたが,最近忙しさにかまけて結構放置してしまっていた...
反省の意を込めて,最初から受け直して見ることにしたのでメモを公開してみようと思う.
最後まで通して受け直す気力が持つといいなー
Welcome
コースの全体像の説明.
What is neural network?
家の大きさから値段を予測したいとする. 家の大きさと値段をプロットすると,それを予測するための直線がなんとなく描ける(図1).

これを別の表現方法で表すと,図2のようにも表せる.

家の大きさをinputとして受け取って,円のなかで何かしらの処理をして,値段をoutputとして出力する. この何かしらの処理が先ほどの直線と同様の関数であれば,家の大きさから値段を予測することができる. この,inputを受け取って,outputを返す円をニューロンという.
このニューロンが複数積み重なってできるのが,ニューラルネットワークである.
Supervised Learning with N.N.
教師あり学習とは,INPUTとOUTPUTの組み合わせが複数与えられた時に,INPUTを正しくOUTPUTに変換する関数を求める学習方法であり,ニューラルネットワークでもよく用いられる.
Why is DeepLearning taking off
ニューラルネットワークは近年の技術的な進歩によってその有用性が高まってきている. 一番大きいのはデジタル化によって存在しているデータの量が増えたことが大きい.
図3にデータ量とパフォーマンスの一般的な関係を載せる.

データが少ない領域では,ニューラルネットワークだろうが他のアルゴリズムだろうが基本的には大きく違いはなく,いかにうまく特徴量を設計できるかによって,その差が生じていた. ここが従来の機械学習は職人技と言われる所以になっていた.
データが多い領域では,逆に,特徴量の設計などは関係なく,大きなネットワークで高い性能が出るようになった.近年のデータ量の増加に伴って,主戦場が移った.
データの量だけではなく,コンピュータの計算能力の向上やアルゴリズムの改善ももちろん大きく寄与している. 大量のデータを扱うのには大変時間がかかっていたが,コンピュータの処理能力の向上やアルゴリズムの向上によって短い時間で処理できるようになったことが大きい進歩の要因の一つになっている.
事業を創る人の大研究を読んだ
「事業を創る人」の大研究を読んだ.
タイトルの通り「人」に着目した新規事業立ち上げに関する本で,独自研究で得られた沢山のデータをもとに考察を進めていくというスタイルの本でとても参考になったので要点をまとめてみようと思う.
本書との出会い
本屋さんでパラパラと新規事業関連の書籍を探していた際に『はじめに』を立ち読みし「あるあるw」と共感し,続きが気になったので,さらに序章を読んだところ「あるあるあるあるw」と深く共感したので購入した.
簡単にまとめると「新規事業ってなんか大変そうだし,あんまり関わりたくないよねw」というのと「新規事業って社内からの風当たり強いよね」という点に共感した.
ターゲット
既存事業がある会社における新規事業立ち上げをターゲットにしている. スタートアップ企業を立ち上げましょうとかそういうことではない点が通底して重要な特徴になっている.これによって様々な軋轢が生まれる.
ターゲットとしているロールは,新規事業を創る人自身はもとより,それを支える上司や経営層を主に狙っているように思う. 本書では「人」として「創る人」「支える人」「育む組織」の3つをあげているが,育む組織の人に遍く届くようにというよりは,むしろ組織をつくる人(つまり経営層)をターゲットにしていると思われる.
本書の立ち位置
新規事業立ち上げに関する書籍は色々ある.カリスマ経営者的な人の自伝に近いような実践系の書籍と学術的な研究に基づく学術書の2つに分けられる. 本書は学術書に分類されるものであり,学術書の中でも新規事業立ち上げについて「人」に着目した点がユニークな点となっているとのこと.
つまり他の書籍とは異なりプロセスから人へ視点を移した点が面白いところ.結局人だよねーという.
第1章
新規事業を取り巻く環境
新規事業を「既存事業でえたモノを活用し,新たな経済効果を生み出す事業」と定義している. 既存事業で得たモノを活用するという点がポイントになる.
ライフスタイルの変化により,新規事業をつくるというのは企業にとって生存戦略として必要不可欠なものになりつつある.
なお,それだけにこれに対する期待はとても大きいようで,「予算的には成功しているプロジェクトであっても経営層の満足度は低く満たされないケースが多い」という面白いデータが示されている.
これ,ゴールポストが動いているということであり,担当者にとっては悪夢でしかない...ちなみにこの問題自体については今後議論されない.
新規事業に必要な能力
新しいアイディアを形にして,それをお客様に届けることができて初めて新たな経済効果が生み出せる.
独自研究で得られたデータから経営者は新規事業を進めていくためには「新しいアイディアを考えて,未知を恐れず,最後まで突き進むことができる」力が必要だと考えているケースが多いらしい.
一方で,新規事業立ち上げ担当が実践を通じて必要だと感じた力は「現場を正しく観察し,上手に他者を巻き込める」力である. 新規事業を立ち上げるために,社内からの理解が得られず苦しむというケースがとても多かった模様.
この結果から,これから新しく担当になる人は社内理解をいかに得るかという点をもっと意識した方が良さそうに思った. これができるかどうかってかなり人間力が問われるテーマだと思う.
特に新規事業はその構造から社内からの風当たりが強くなりがちだし,孤立しがち.しんどいことも多い. その証拠に,新規事業を去っていく人の理由は「事業自体がうまくいかなかったことよりも,新規事業をめぐる構造によるもの」が多い.
まとめ
新規事業はアイディアそれ自身よりもいかに周囲を巻き込むかが大事であり,そこに人の力が問われる.さらに,新規事業の構造上,しんどいことが多いので,折れない心の力も大事.
いかに心が強い人でもサポートがないと折れてしまうので,支える人や組織がさらに大事.それらもマルッと含めて,人が大事ということ.
第3章
創る人に求められるスタンス
新規事業は結果が出るかどうかわからないものであり,業績志向になりすぎても結果が出るかどうかはわからない. むしろ事業を出そうというプロセス自体から学びを得て,それを糧にさらにブラッシュアップできるような成長志向のマインドセットが必要.
ゼロから試行錯誤しながら形作る経験からしか学べないことは大きい.これを学び,生かしていくマインドセットが重要.
事前知識があることの優位性
前述の通り,新規事業の構造からきているしんどさが多いので,嵌る可能性のある落とし穴が独自研究の成果から見つかっている. 11の問題とそれをまとめた4つのジレンマという形でそれらが以降の章でまとまっている.
これを知っておくことで,自分が今置かれている状況を俯瞰的に理解できるし,それによって「これは自分だけの固有の問題ではなく構造上の問題なんだ」とリフレーミングでき,前向きに問題に取り組めるようになる.
これが本書の大きな価値になっていると思う.
第4章
前述の11の問題について解説がある.が,個別具体的なこうしたら良いというのは残念ながら示されていない. 示されてはいないが,問題の粒度が大きいため,個別具体的な解決は状況によるところが大きいからこれは仕方ないと思う.
大事なのは,こういう問題が実際に起こりうるだろうということを理解しておくこと.
「既存事業部門からの批判」とか「新規事業プランを生み出せないジレンマ」あたりがとてもとても身につまされる.
既存事業部門からの批判
新規事業の人たちは何やってるかわからんというところが原因になってこの問題が起こるように思う. 何やってるかわからん人たちが,自分たちが必死に生み出した利益を食いつぶしているように見えるという構造が,この批判をうむ.
進め方や情報発信を考えてやっていかないと,簡単に孤立しまっせというお話.つらい...
新規事業プランを生み出せないジレンマ
創る人は,その事業が軌道に乗るまではできていない状態が続くわけで,できない自分の姿に苦しみ続けることになる.
第5章
新規事業を創る人はそんな感じで孤立したり,しんどかったりするようなので,それを折れないようにサポートする組織風土が必要だというお話.
事実として,他部門が新規事業を応援しようという組織風土は新規事業の業績を有意に高め,新規事業をお金の無駄だと思っている組織風土は業績を有意に下げるというデータもある.
若干ポジショントーク的に感じなくもないけど,データが出ている以上そういうことなのかなという印象. とはいえ,組織風土は片方が頑張って作れば良いものではもちろんないとも思う. 創る側の人も,自身がどう見られる可能性が高くて,実際にどう見られているのかということを常に自問して,事業を成功させるために社内の周囲との関係性づくりを怠ってはいけないんだと思う.
読了後まとめ
本書では人の側面が強く論じられていたけど,もちろん技術的な面やアイディアが出せるかという面も大事.というかそっちこそが前提だとは個人的に思う. その上で人としての力も求められるということで,新規事業を成功させるためには高い総合力が求められる.
そのための補助輪として本書は有用だと思う. 事前に予期できるだけで心構えができるし,準備もできる.自分だけが抱える問題じゃなくて構造上起こりうる問題なんだと捉えられるようになる点も,将来本書に助けられるところがあるかもしれない.
ところで,人間力ってどうしたらつくんでしょうね........

- 作者: 田中聡,中原淳
- 出版社/メーカー: クロスメディア・パブリッシング(インプレス)
- 発売日: 2018/01/29
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (2件) を見る
「○○がない」ということについて最近考えること
「○○がない」という言葉を聞くたびに、最近思うことがある。
「○○がない」って、一見問題提起っぽく見えるけど、その実はただの事実を述べてるにすぎない。
これをどうやったら解決すべき問題や、より良くするためのアクションを誘発する問いにできるか?を考えてみたい。
たとえば?
「hogehoge分析をしてみた結果、第N象限に関する取り組みがないです」とか「UnitTestが無いです。テストコード自体も、テストコードを書く文化自体もないです」みたいなやつ。
どういうこと?
「○○がない」ってのは事実であり、○○が存在していないってことを指摘している。
「問題」というのはなんらかの不都合があるから解決する対処だとすると、「○○がない」という事実が、そのまま全てなんらかの不都合に結びつくものでは無いと思う。
例えば、「弊社には薬剤師がいない」という事実があったとして、弊社はソフトウェアメーカなので別段不具合はないのでそれは問題ではないと思うわけで。
このように、「ない」という事実は問題に直結しない。
ここまで極端な例ではなくても、「みんながあったらいいかも」と思うような内容であっても、様々な制約や優先事項から取り入れていないケースもあるかも。 例えば、「弊社にはテレビCMがない」という事実があり、テレビCMがあればもっと売れるようになるかも?という期待はあるけど、予算や理念、効果についての考えなどからそういう選択をしている(?)ものであり、それは問題ではないと思う。
このような切り分けなく「○○がない」という事実自体を問題として扱うと、それの解決方法は「○○がある」という状態を作ることにもなる。 その結果、「○○がない」を裏返した「○○がある」状態をやみくもに目指すことになり、有限なリソースをへんな配分で消費してしまったりすることになる。
さらに、「○○がない」事実を「○○がある」状態に変えたところで、その奥にある問題を発見できていないので、真の問題に対するカイゼンが進まないと言う問題もある。
前述の「テレビCMがない」こと自体を問題として捉えてみると、それを解決するためには「テレビCMをうつ」ということになる。 が、解決するべき問題って、売り上げが少ないとか購買層からの認知が低いとかそういうことですよね。
購買層からの認知が低いことが問題であれば、テレビでマス向けに広告打たなくてもいいかもしれないし、売り上げが少ないことが問題であれば、もっと営業活動に投資するとかあるかもしれない。利益が低いみたいな問題であればCM打つことによって余計費用がかさんでマイナス効果が出るケースもあるかも。
じゃあどうしたらいい?
問題まで落とし込んで考えるべきだと思う。 「○○がない」ことでどんな不都合があるのか?
テストコードがないから、どんな不都合があるのか?みたいな。
テストコードがないことで、テスト工数が余計にかかっているとか、バグが流出しているとか、リファクタリングできないとか。そういう具体的な問題をベースに考えるようにしたい。 そうしないと、ただ「ある」状態をやみくもに目指すことになると思う。
問題まで落とし込めば、ある状態を作る以外のもっと良い解決策にたどり着くかもしれない。
おちは?
ないです。
会社でハッカソンをやってみた 進め方編 2
前回記事の続き。 ハッカソンを行う上で「何を作るか?」の決め方について。
結論から言うと、メンバーに任せっきりで特段問題はなかった。
ハッカソンプレ実施で得た学び
前回記事のアイディアソンのフレームワークを運営メンバーだけで実施し、短縮版のハッカソンを行った。 その結果、以下の通りの問題が浮かび上がった。
- お客様ロールの人の課題を解決することに固執し、技術的のアップデートという点が追及できなかった
- SI的なお客様のお困りごとをヒアリングし、それを解決するような取り組みになってしまい、自分たちで考えて進めるワクワク感が目減りした
今回は製品開発に活かしたり実用的なアイディアを出すことが目的ではなく、新しいことをやることや、自分たちで主体的にアイディアを出して開発をすることに重きを置いていたため、前述のフレームワークでは上手くはまらないとの結論に至った。
チーム内で相当議論を重ね、最終的には「進め方を決めないで各チームに任せる」という一見丸投げなアイディアに至った。 一応ここに至る前に、チーム内で下記の方法を試しており、当初の進め方よりは目的に沿ったアイディア出しが出来ることを確認していたが、それでもやはりお仕着せ感が拭えず、最終的には各チームに任せるという結論に至った。
ただ、完全に任せる形では事故る可能性があるので、各チームに運営メンバーが付き添い、上手く進まなそうであれば下記の進め方を紹介し、事故らないようにフォローする体制を敷いていた。
改良した進め方案
ターゲットについて
ターゲットを未来の時点でのお客様と設定する。これによって今のお客様の御用聞きにならず、自分たちで未来の時点でのお客様を想像しながらアイディア出しを行うようになる。
どんな未来か?を考える
どんな時点での未来をターゲットとするかを考え、その時点で起きていそうなことを考える。 たとえば2020年をターゲットとした場合、オリンピックがあり、国外の人たちが沢山来日するとか。 もっと先であれば労働人口の減少や働き方改革の推進による変化(在宅ワークが増えたりフレックスが増えたり)など、どんな未来になっているかを考える
どんな課題か?を考える
その上で、お客様はどんな課題に直面するだろう?という点を考える。 そしてそれを解決するためにはどんなものが必要だろうか?と考えて、アイディアとする。
結果
事故るのでは?というのは、はっきり杞憂だった。 全てのチーム(9チームとも)が自分たちの進め方を見つけ、とても興味深く面白いアイディアを出すことができた。 こればっかりは参加メンバーの能力によるところが大きいが、うちのメンバーはみなその能力に長けていたんだと思う。