Foundations of Convolutional Neural Networks
CouseraのDeepLearningのコースを受けている際の講義メモ.
https://www.coursera.org/learn/convolutional-neural-networks/home/week/1
今週はConvolutional Neural Networksということで画像の処理なんかによく使われるCNNのお話.
Coumputer Vision
コンピュータビジョンはDeepLearningによってかなり大きく進展した分野. 画像に写っているものを識別するような画像認識,画像から物体がどこにあるかを検知する物体検知,ある画像を別の画像のスタイルに変換するNeural Style Transferと言ったタスクがある.
画像は大変大量の情報を持つため,通常のニューラルネットを用いようとするととても大きなInputになる.これは計算コストの増大やOverfittingのリスクなどを引き起こす. CNNはこの問題に対してアプローチしている.
Edge Detection Example
CNNの前に,画像処理の分野でよく行われる,エッジ検知を見ていこう.
所望の画像に対して,特定のフィルタをかけると,どこにエッジがあるかを検出することができる. フィルタをかける処理のことを畳み込みと呼ぶ.
縦方向のエッジを検知するためのフィルタと,そのフィルタによってエッジが検知されている例を図1に示す.
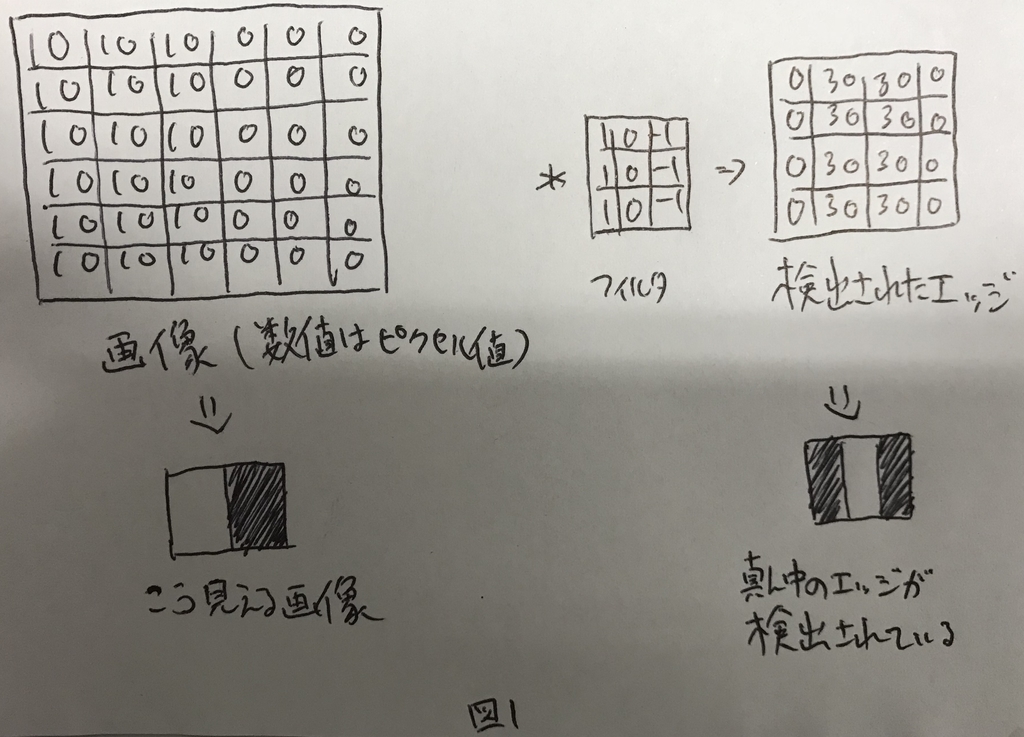
More Edge Detection
縦方向のエッジだけでなく,フィルタの形によってはいろんなエッジを検出できる.
例えば図2のフィルタでは横方向のエッジを検出することが可能.
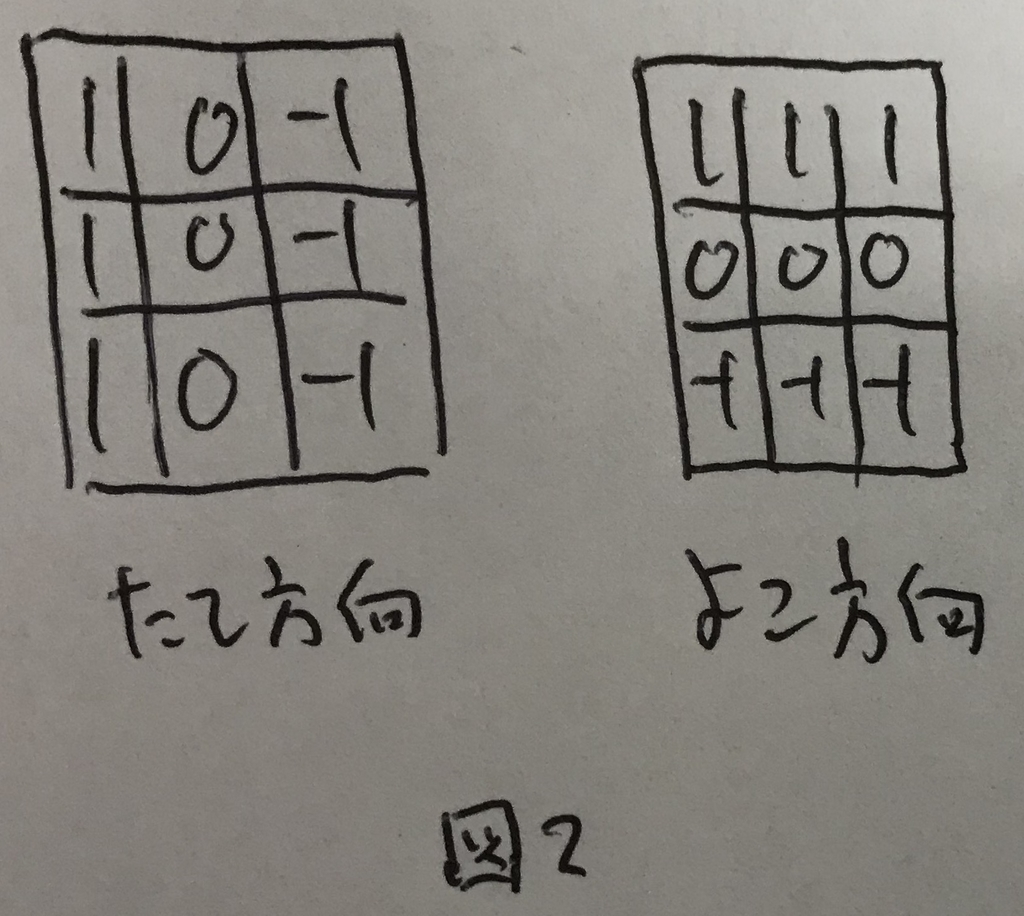
このように,フィルタの形によって検出できる特徴は異なる.
CNNでは,フィルタの各値をパラメータとして,画像の情報をよりよく表せるように学習を行う.
Padding
図1の例のように,畳み込みを行うと,画像が縮退する. フィルタをたくさんかけると画像がどんどんどんどん小さくなってしまう. これをコントロールするために,Paddingという技術がある. また,畳み込みを行う際に,左上のピクセルは畳み込みの計算時に1度しか活用されないが,中央のピクセルはフィルタの大きさ分だけ活用されるということもあり,画像の端っこの情報がうまく活用できていない.これもPaddingによって解決できる.
Paddingとは,畳み込みを行う前に,元の画像の淵にピクセルを埋めてしまうことを示す. 元の画像の外堀にPadding量の分だけピクセルを追加してあげる.この時,ピクセル値は0にするのが一般的.Paddingのイメージを図3に示す.
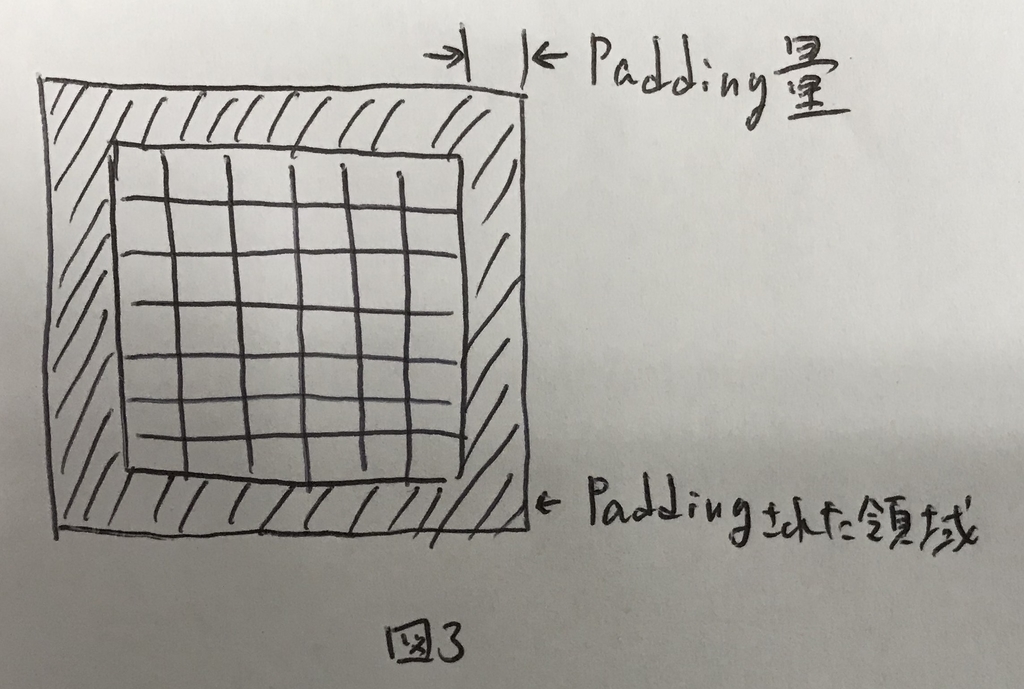
図3の斜線部分がPaddingで0埋めされた領域であり,どのくらい埋めるかはPadding量で決まる. Padding量が1だったら上下左右に1ピクセル追加するし,2だったら2ピクセル追加する.
Pagging量が0の場合をValidパディングと呼び,Padding量が「Paddingした結果,フィルタを畳み込んだ際に得られる画像の大きさが畳み込み前と変わらない」場合をSameパディングと呼ぶ.
なおパディング量をpと表記する.
Strided Convolutions
これまで,畳み込みは元の画像に対してフィルタを1つずつずらして行う想定で進めてきた. 実際には,これを1つではなく,2とか3とかずらすこともある.
このずらす幅のことをストライドと呼ぶ.
ストライドをsと表記した時,畳み込み後に得られる画像の大きさは,パディング量pを用いて図4で表せる.
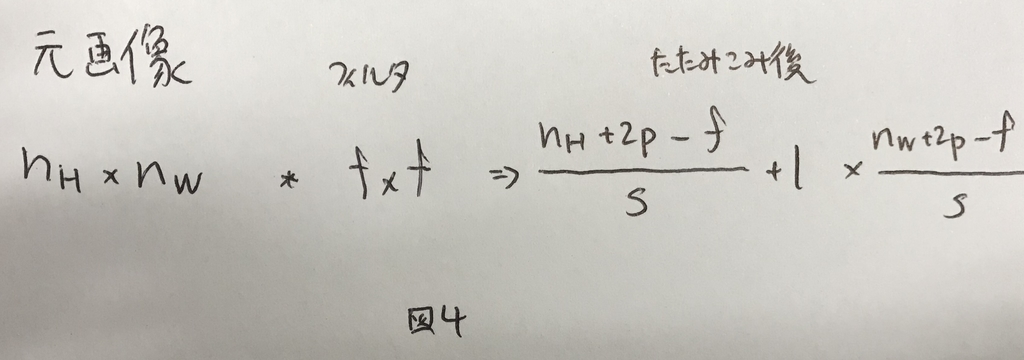
なお,畳み込み後のサイズは整数にならないケースもある.その場合は切り捨てる.
つまり,ストライドsで大きさfのフィルタをかけていき,もしもパディング量pでパディングされた画像からフィルタがはみ出す場合は計算を行わずに次に行くというようなフィルタのかけ方を行う.
Convolutions Over Volume
今までは2Dの例を見てきた. 画像を扱う際には,カラーチャネルがあるのでカラーチャネル(R/G/B)を含めた3D(縦×横×チャネル)の例を見て行く.
3Dの場合,畳み込みするフィルタも同じチャネル数が必要になる. 畳み込みは全てのチャネルについて透過的に実施され,最終的に得られるのは1チャネルの結果となる.
つまり,図5のようなイメージになる.
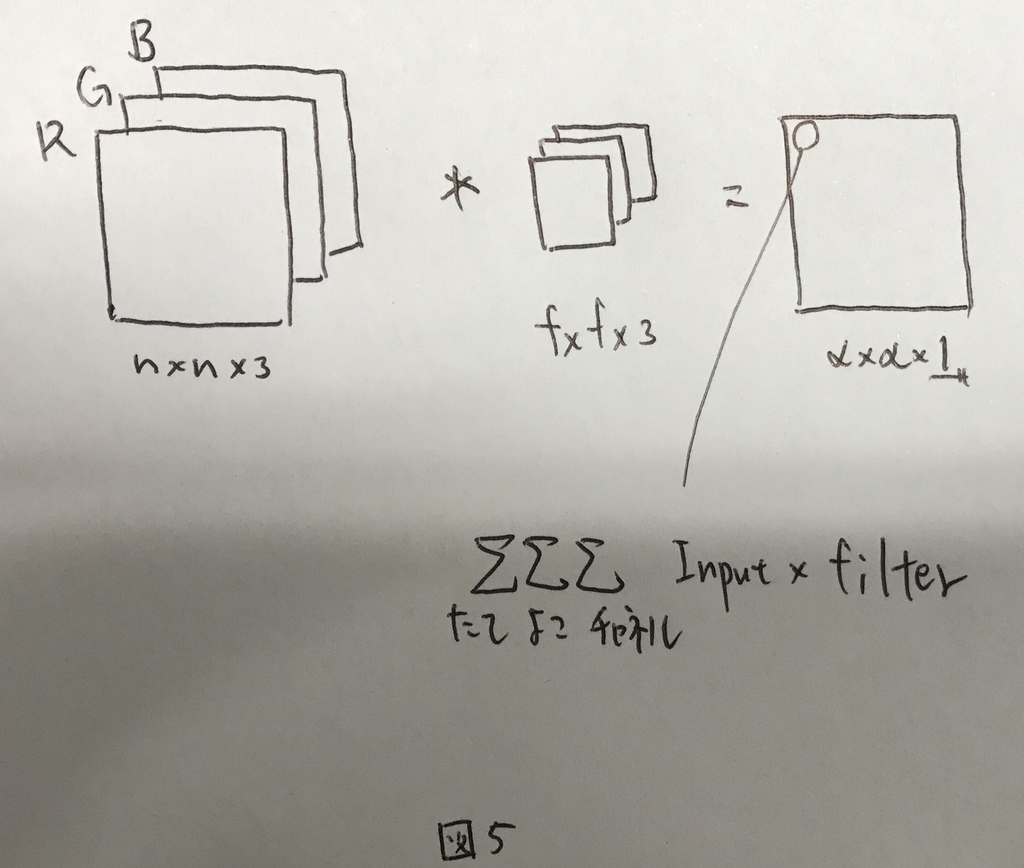
さらに,フィルタを複数かける例を考えると,図6のように最終的な出力も3D(たて×よこ×フィルタ数)になる.
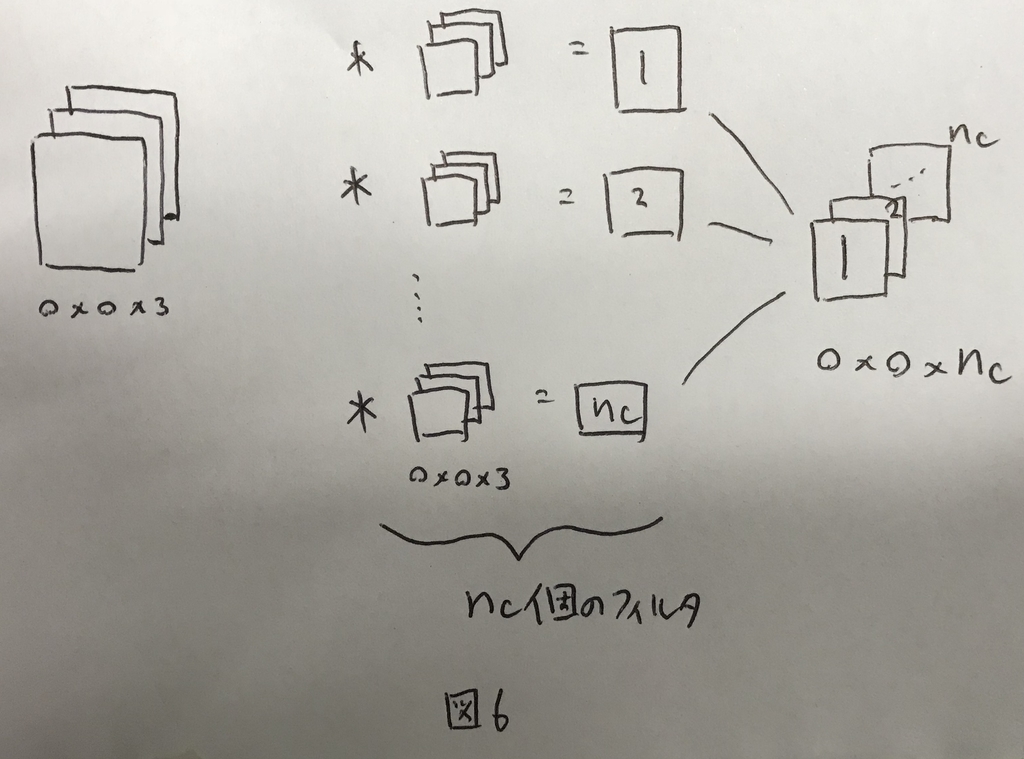
この,フィルタ数(nC)のことを,チャネル数と呼ぶことにする.
One Layer of a Convolutional Network
CNNの1レイヤーサンプルを図7に示す.
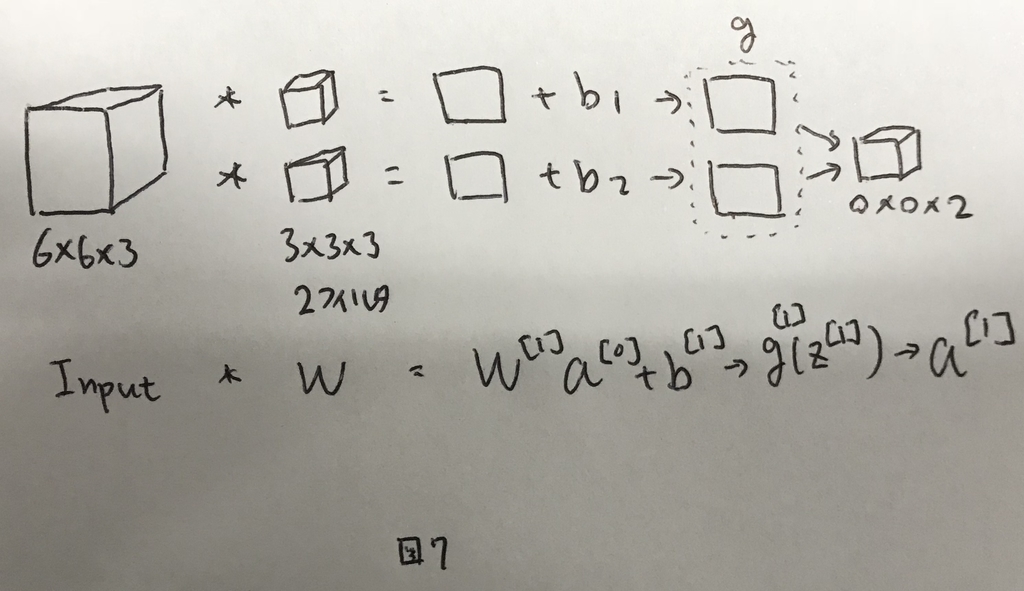
ここで,学習対象となるパラメタの個数は,Wの総数(3×3×3)とバイアス1を足した28個になる. さらにフィルタが2個だとすると,それぞれにバイアスが必要なので,28×2の56個が総数である. これらのフィルタを画像の全ての部分に共通して使って行く.後述するが,この特徴によりCNNは比較的学習対象のパラメータが少なく,過学習を起こしにくいという特徴がある.
CNNで用いる表記を図8にまとめる.
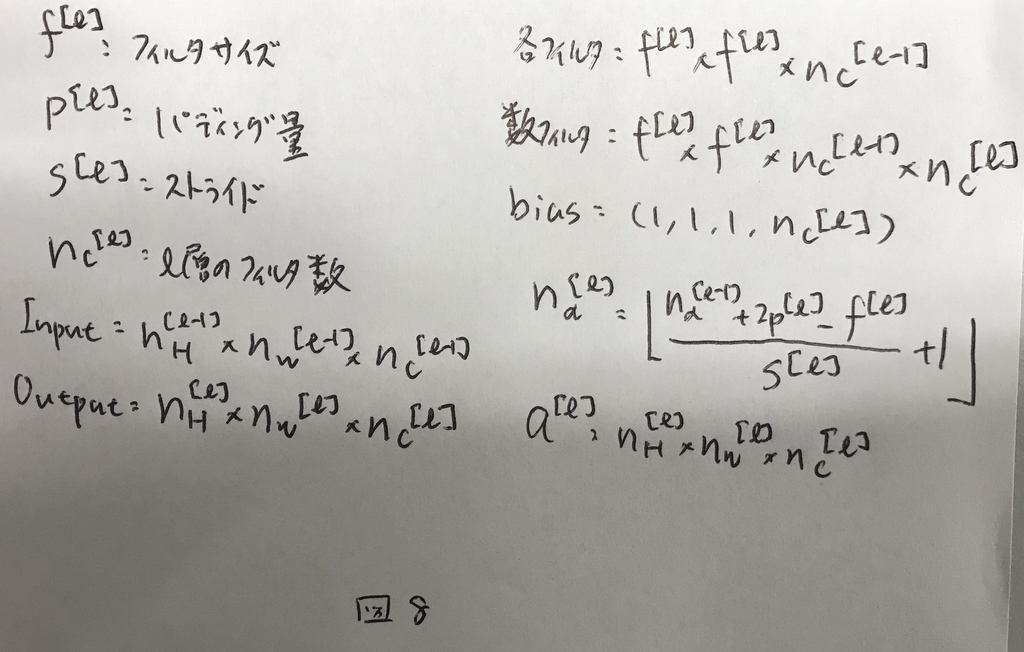
Simple Convolutional Network Example
CNNでは,3つのレイヤーを組み合わせることができる.
- 畳み込み層
- プーリング層
- 総結合層
Pooling Layers
プーリング層では計算量を減らすことと,特徴量をロバストにすることの2つが実現できる. プーリングには最大プーリングと平均プーリングの2つがある.
最大プーリングの計算イメージを図9に示す.
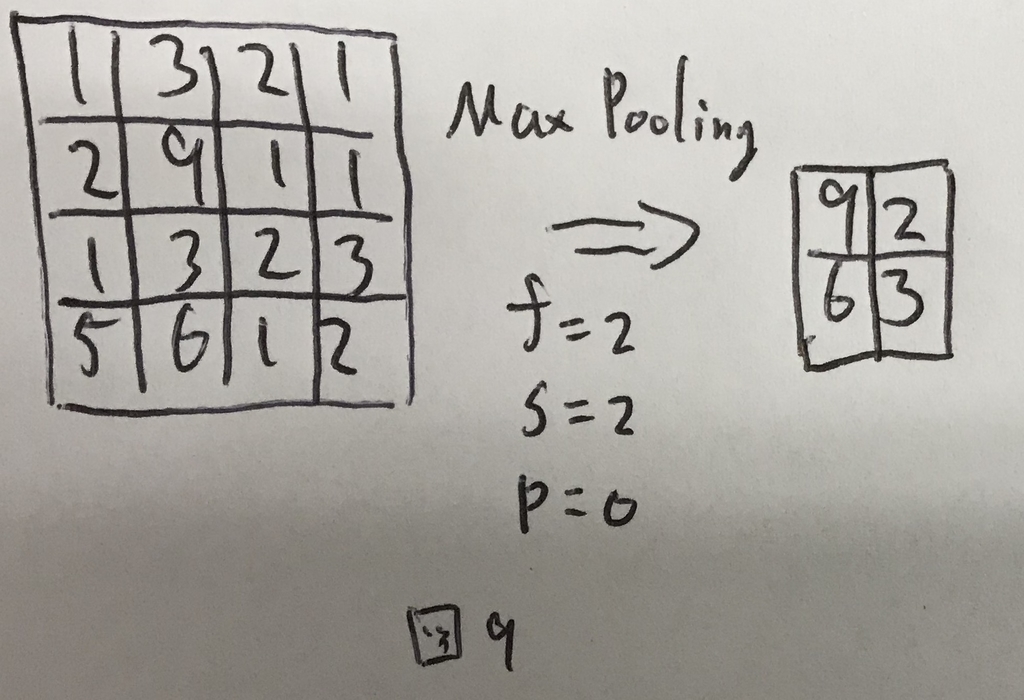
このように,フィルタ範囲内の最大値を返すものが最大プーリングである. 最大値を返すフィルタなので,学習するべきパラメータを持たないという特徴がある.
平均プーリングは,その名前の通り,平均値を返す.
プーリングはチャネルごとに計算され,チャネル数方向への縮退は起こらない.
Maxプーリングは実用的に効果が確認されており,よく使われる技術である.
CNN Example
これまで見てきたものをまとめて,CNNのサンプルを図10に示す.
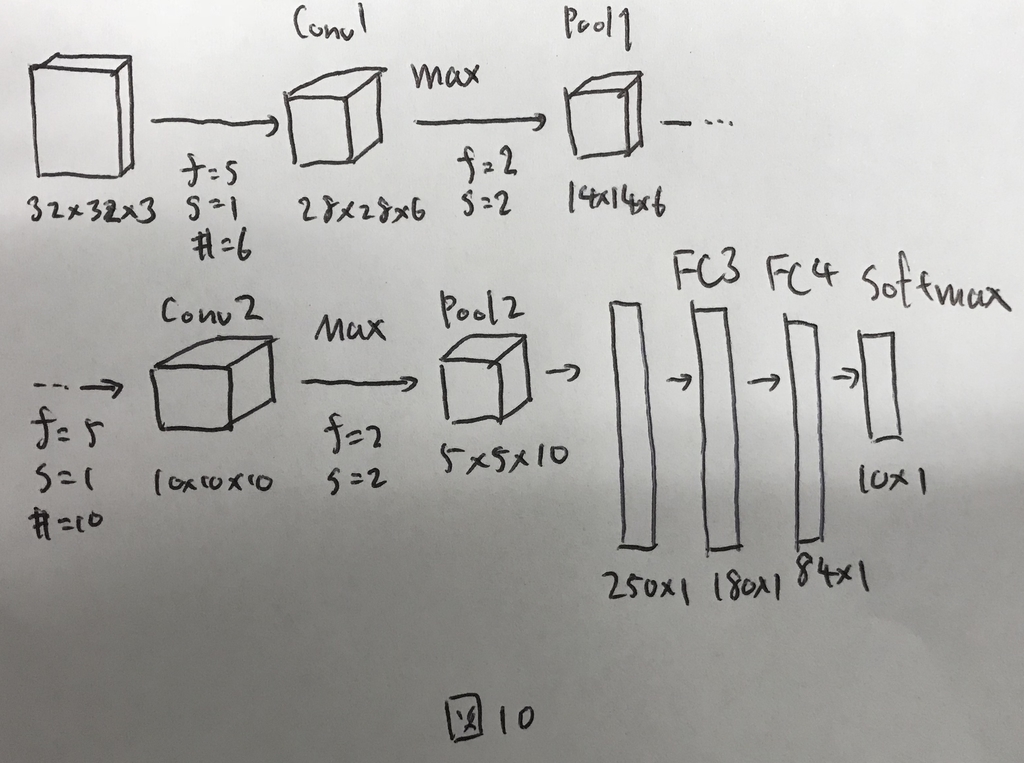
ここで,レイヤーの数え方には2つの流派がある. まず一つ目は,畳み込み層やプーリング層をそれぞれ1レイヤーとして数える方法である. もう一つ目は,学習すべきパラメータを持つもののみをレイヤーとして数える方法で,その場合はプーリング層はカウントしない. 本講座では後者の数え方を採用している.
図10のように,CNNでは設定すべきHyperparameterが無数にある. アプリケーションを構築する上では,一から構造を考えるのではなく,論文などで研究者がうまくやっている方法を参考にして活用することがおすすめ. 一般的なガイドラインとしては,nHとnWは少しづつ小さくするように設定し,nCは少しづつ増えるように設定して行くと良い.最後に総結合層を持ってきて,結果をえるように設計する.
Why Convolutions?
CNNの利点は大きく2つ. パラメータ共有とスパース結合という特徴である.これらがあるので,過学習しにくく,計算コストも低い.
パラメータ共有
パラメータ共有とは,画像の全領域に共有した同じフィルタを適用するということである. 32×32×3の画像にフィルタをかけて,28×28×6に変換する処理を考える. CNNでは,フィルタはf=5でフィルタ数は6で良いので,バイアス合わせて156個の値からなる. これが通常のNNだと32×32×3×28×28×6+1個の値からなるフィルタが必要であり,とてもじゃないが計算しきれない.
画像の処理などは特に,エッジ検出など基本構造を検出するためのフィルタは,画像の一部だけでなく全体で有用であるという特徴があるため成り立っている.
スパース結合
とある層のとあるピクセルは,直前の層の一部のピクセルとしか結合していないということをスパース結合であるという. 図11のように,とある層は直前の全ての層の計算結果ではなく,一部の層の計算結果からのみなる.
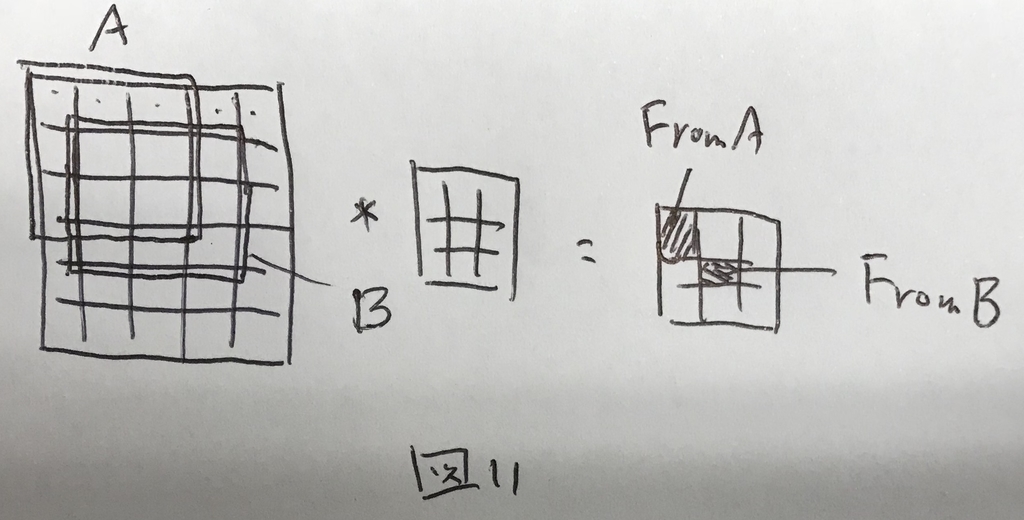
これにより,計算コストが少なく,過学習を起こしにくいという特徴が生じる.