Hyperparameter tuning, Batch Normalization and Programming Frameworks
CouseraのDeepLearningのコース2つめ最終週. 学習メモです.
Hyperparameter tuning
Tuning process
これまで見てきたように,チューニングするべきhyperparameterはいっぱいある. これをうまくチューニングするためのガイドラインを説明する.
チューニング対象
チューニングするべき対象は以下の通り.
- 学習率α
- Momentumのβ
- Adamのパラメータβ1とβ2
- Layer数
- 隠れユニット数
- 学習率減衰の係数
- ミニバッチサイズ
このうち,一番大切なチューニング対象は学習率αであり,積極的にチューニングを行う. 次に大事なのはMomentumのβと隠れユニット数,ミニバッチサイズである.これらもチューニングする. そのあとに大事なのがLayer数と学習率減衰の係数であり,これはあまりチューニングしない. 最後に,Adamのためのパラメータはほぼチューニングせずにデフォルトの値を用いることが多い.
チューニング方法
単純化するために2つのパラメータを考える.
従来のやり方では,例えばN回の施行ができるとすると,2つのパラメータから√N個ずつ候補を決め,それらをGrid的に全探索して良いものを最適な組み合わせとして使っていた. この方法では,各パラメータについて√N個のパターンを試すことしかできないため,実はあまり効率が良くなかった.
そこで,DeepLearningの世界では,Grid的な探索は行わず,ランダムにN個の候補をパラメータ空間から取り出して探索を行う.こうすることで,各パラメータに対してN個の値を施工することができ,効率が良くなる.
さらに,必要に応じて粗密サンプリングを行う. 粗密サンプリングとは,2つのステップからなるチューニング方法で,
- まずパラメータ空間の中で荒く候補点を決めて探索する
- 良い結果が得られたサンプル付近からさらに重点的に候補点を抽出し,改めて探索する
という方法である.
闇雲に全探索するより効率が良い.
Using an appropriate scale to pick hyperparameters
必ずしもリニアスケール上でランダムサンプリングすれば良いというわけではないというお話.
例えば隠れユニット数について,だいたい50-100の間くらいに正解があるだろうという状況であればリニアスケール上でランダムにサンプリングして探索すれば問題ない.
一方で,学習率αについて,0.0001から1くらいの間に正解があると思われるときに,リニアスケールでランダム抽出すると効率がよくない.
何も考えずにランダム抽出すると抽出される候補の割合が,0.0001~0.1が10%,0.1~1が90%になる. αのようなレンジの場合,そうではなく,0.0001~0.001と0.001~0.01と0.01~0.1と0.1~1の間のサンプルの割合を等しくしたい.そんな時はリニアスケールではなくログスケール上でのランダムサンプリングを行う必要があるので注意が必要.
Hyperparameters tuning in practice
実践的に効率的にチューニングをする方法について.
使える計算リソースによってチューニング方法を選択する必要がある. 選択肢は2つあり,「Baby sitting one Model」と「Parallel Model」である.
Baby sitting one Model
計算リソースが限られているケースで選択する. コスト関数を観察しながら,学習中にパラメータを手動で調整するようなモデル. 最初はランダムに初期化したパラメータを使い,学習を開始する. コスト関数の値を観察しながら,手動で学習率をあげたり,下げたりする.
このアプローチは別名パンダアプローチとも呼ぶ. パンダは子供が少なく,1人の子供を大切に育てるため. 手塩にかけてモデルを育てていくイメージ.
Parallel Model
潤沢に計算リソースを持っているケースで選択する. 複数のモデルを同時に別パラメータで学習させ,その中から一番良いものを選び出す方法.
前述のパンダアプローチに比べてキャビアアプローチというイメージ. チョウザメは一度に大量の子供を産むので,一人一人を大事に育てることはしない.
Parallel Modelも同様に,たくさん施工して良いものだけを選択する. Baby sitting one Modelのように1つに手をかけたりはしない.
Batch Normalization
バッチ正規化という方法について説明する. バッチ正規化はネットワークをロバストにすることができるため,hyperparameterのチューニングが楽になる.また,学習を高速化する効果も望める.かなり重要なアルゴリズムの1つ.
Normalizing activations in a network
以前,ロジスティック回帰において,Inputとなるベクトルを正規化することでモデルの学習が高速化されることを見てきた.
ニューラルネットワークはロジスティック回帰のノードを積み重ねたようなものであり,各ノードへの入力となる部分を正規化することで学習を早めることができるのではないだろうか,というのがバッチ正規化のアイディアとなる.
なお,実際には各ノードへの入力a=g(z)の正規化ではなく,zの正規化を行うほうが実践的によく用いられる手法であるため,zの正規化を行うものをバッチ正規化として説明する.
バッチ正規化は,ニューラルネットワークを学習する過程のなかで,各隠れ層について図1のような処理を行う.

ここでΓとβはそれぞれモデル学習時に学習するものであり,学習方法については後述する. ここで大切なのは,Zは一度平均0,分散1に正規化された後で,学習されたΓとβを用いて平均と分散が補正されているという点である.
この補正されたZを用いてニューラルネットワークの学習を進めることになる.
Fitting Batch Norm into a neural network
ニューラルネットワークの中にバッチ正規化を取り入れた全体像を説明する. バッチ正規化を取り入れる前のニューラルネットワークと取り入れた後の違いを図2に示す.
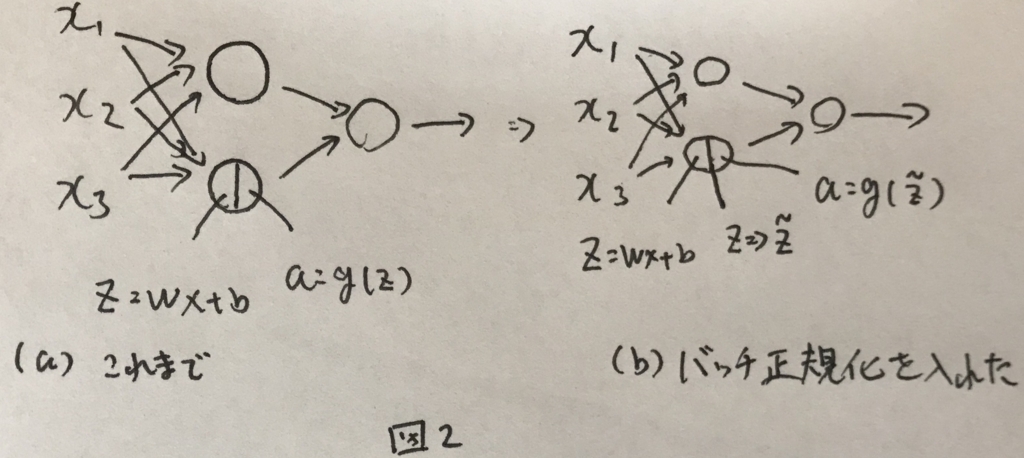
ざっくりこんなイメージ.
学習したいパラメータは図3のようになる.

ただし,バッチ正規化によって,Zは一度平均0で分散1の値に変換される. この変換において,平均が0に補正される際に,バイアス項bが0になる. なので,バッチ正規化時には,bはパラメータから意図的に外されなくてはいけない,
これを考慮して,正しい学習対象のパラメータは図4のようになる.
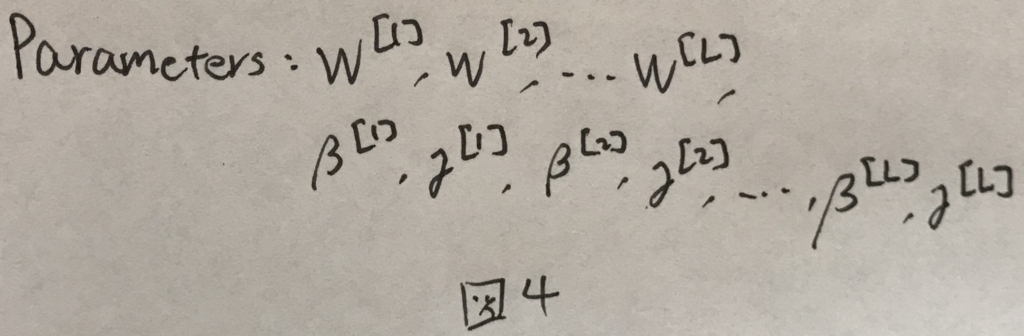
ミニバッチへの適用
ミニバッチ勾配法へバッチ正規化を適用する際には,平均と分散の計算をミニバッチに含まれるデータのみで毎回計算すること.一旦全ての教師データから平均と分散を計算して補正に用いるようなことはせず,あくまでミニバッチの中でのみ完結させる.
ミニバッチ勾配法へバッチ正規化を適用したアルゴリズム(1epoch)を図5に示す.

なおこれはスタンダードな勾配法だが,MomentumやRMSpropやAdamについても同様である.
Why does Batch Norm work?
バッチ正規化を行うことで,深い層が入力の変化についてロバストな耐性を得ることができるため,バッチ正規化は有効.
一方副作用もあり,ミニバッチサイズが小さい状態でバッチ正規化を行うと正則化と同様の効果が発生する.ミニバッチサイズを大きくしてバッチ正規化を行うことで正則化効果を下げることは可能.
Batch Norm at test time
学習したモデルを用いて予測を行う際には,1つの入力を処理して出力を得る. 扱う入力は1つなので,平均と分散を求めることができないのでどうするか.
この問題を解決するために,学習時に計算した平均と分散を使う.
学習時には,各バッチごとに各レイヤーの平均と分散が得られる. この各レイヤーごとの平均と分散から指数移動平均を求めてとっておき,それを予測時の平均と分散として用いることでこの問題を解決することができる.
Multi-class classification
これまでは,binaryClassificationの例を見てきた. ここからは多クラス分類について見ていく.
Softmax Regression
これまでは,「この画像は猫か?」というような問題を扱ってきた. ここからは「この画像は猫か犬かひよこかそれ以外か?」という問題を扱う.
上記の例は4つのクラスへの分類と表現できる. 正解ラベルが,猫であれば1,犬であれば2,ひよこであれば3,それ以外であれば0だとする.
これを分類するネットワークは図6のように表せる.
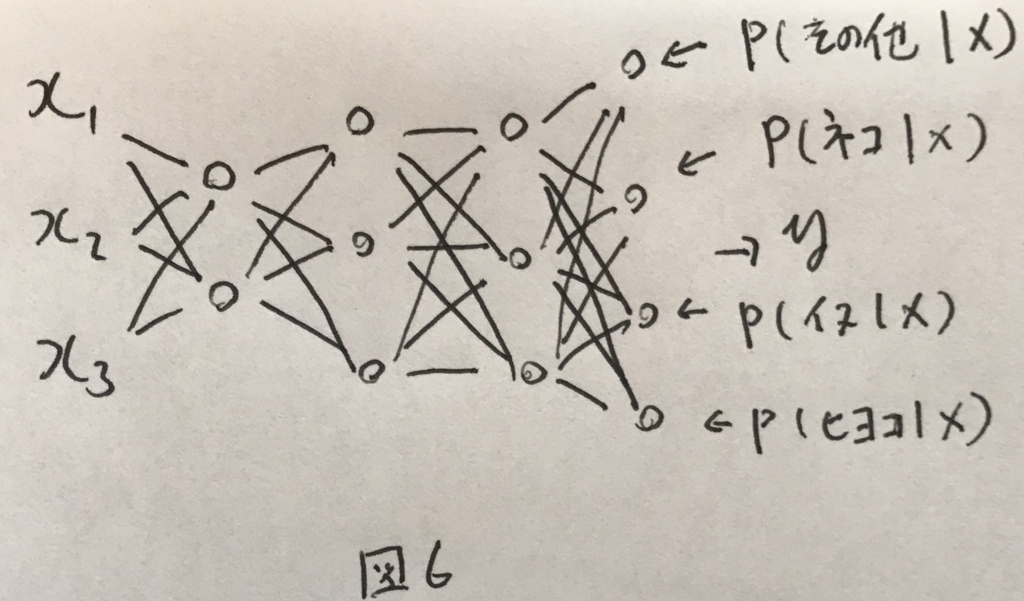
最終的な層がクラスの分になっている点がこれまでとの違いである. 最終的な層には,各クラスである確率を表現させたい. 例えば,0番目は入力がクラス0(つまりその他)である確率を表現させ,1番目には入力がクラス1(つまり猫)である確率を表現させる.
これを表現させるために最後の層の活性化関数としてよく用いられるのがsoftmax関数である. softmax関数は図7の式で表せる.全てのクラスについて確率を足し合わせると1になる特徴を持つ.
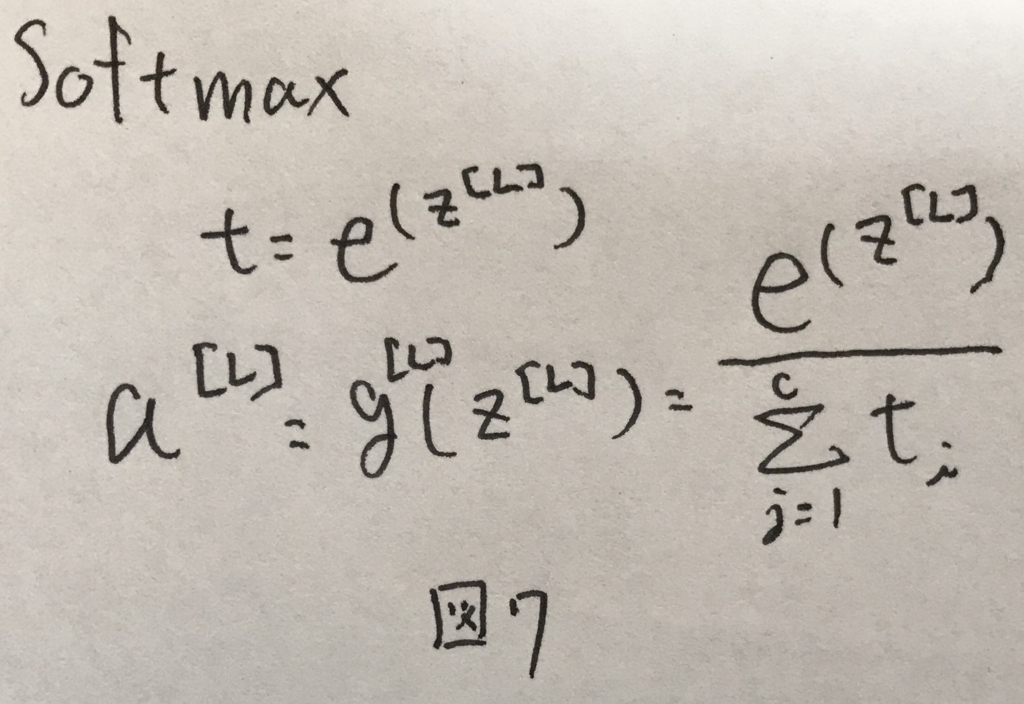
Training a softmax classifier
多クラスの場合のネットワークの学習について. 損失関数とコスト関数は図8のように表せる.
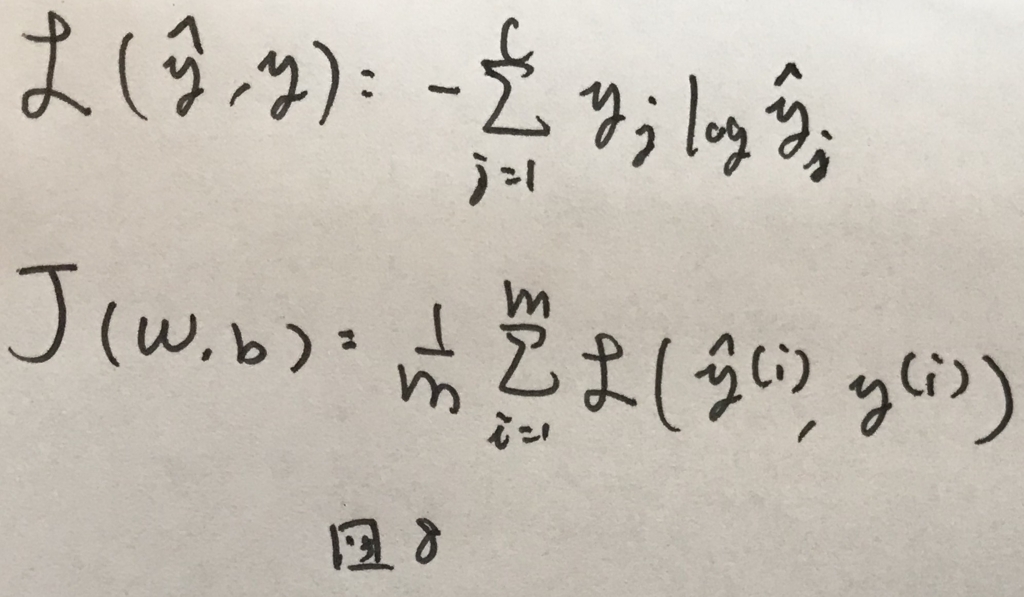
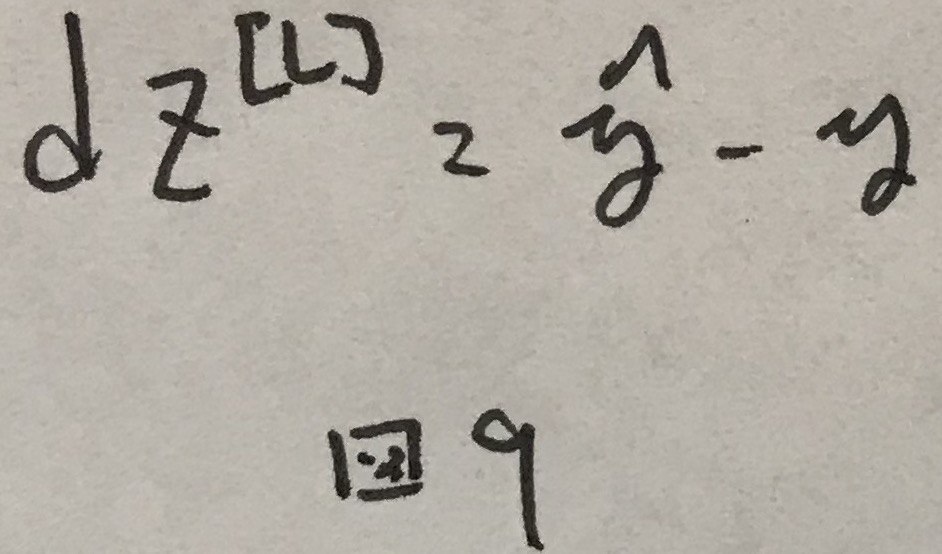
このコスト関数において,誤差逆伝播の際に使われる一番はじめの誤差は図9のように求まる.
あとはいつも通り学習を進めれば良い.
Introduction to programming frameworks
DeepLearningのためのフレームワークの説明. 割愛.