Shallow neural networks
CouseraのDeep Learningコースの第1コースの3週目
Neural Networks Overview
ニューラルネットワークの大枠の説明. 以降の章で話されることが端的に出てくる.
Neural Network Representation
前回学んだロジスティック回帰のノードを複数結合させたようなものをニューラルネットワークと呼ぶ(図1).
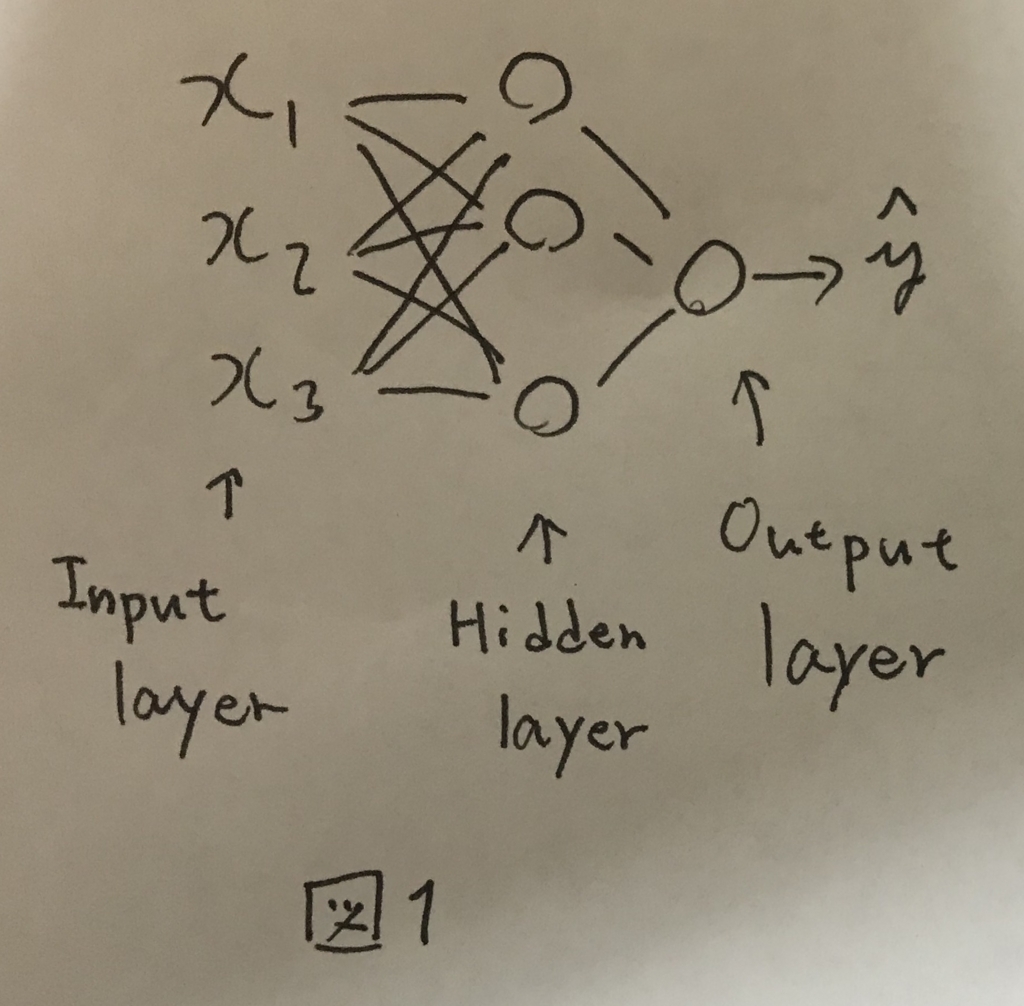
入力のノード群をInput Layer,出力のノードをOutput Layerと呼び,真ん中の層をHidden Layerと呼ぶ.
トレーニングセットにはInputLayerとOutputLayerのデータのみが含まれ,HiddenLayerの情報は含まれない.そのためHiddenLayer(隠れ層)という表現で呼ばれる.
図1のニューラルネットワークは2層のニューラルネットワークと呼ばれ,慣習的にInputLayerはカウントしない.
各レイヤーの出力する値は図2のようにそれぞれa^[i]で表される.
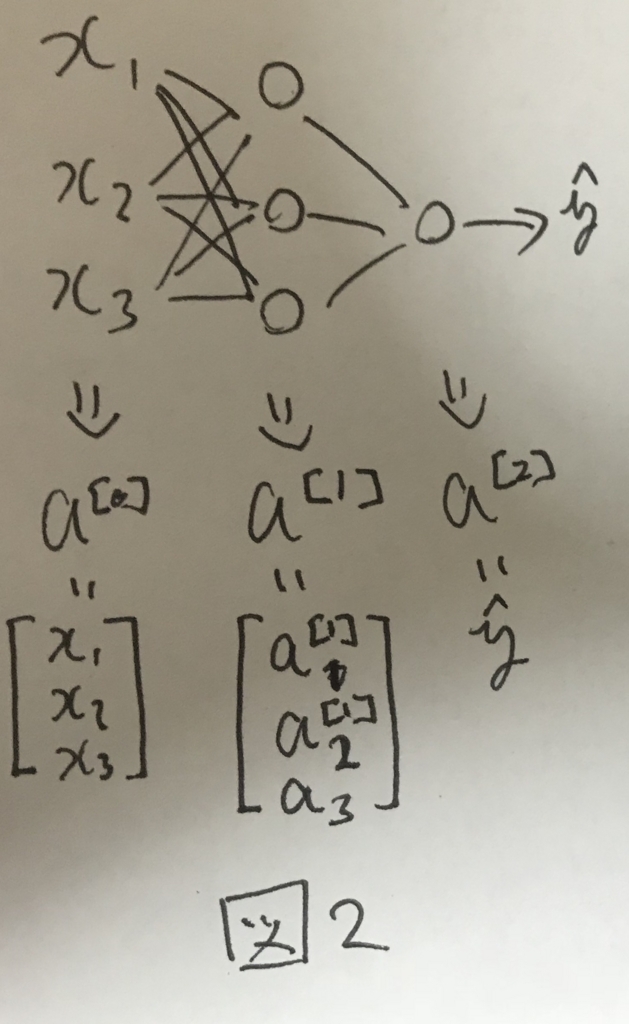
Computing a Neural Network's Output
各ノードは自身へのインプットと重みの計算と活性化関数の処理を行う. 活性化関数は後述するが,ロジスティック回帰のSigmoid関数をイメージすればよい.
図3に第一層で行われる処理のイメージを示す.
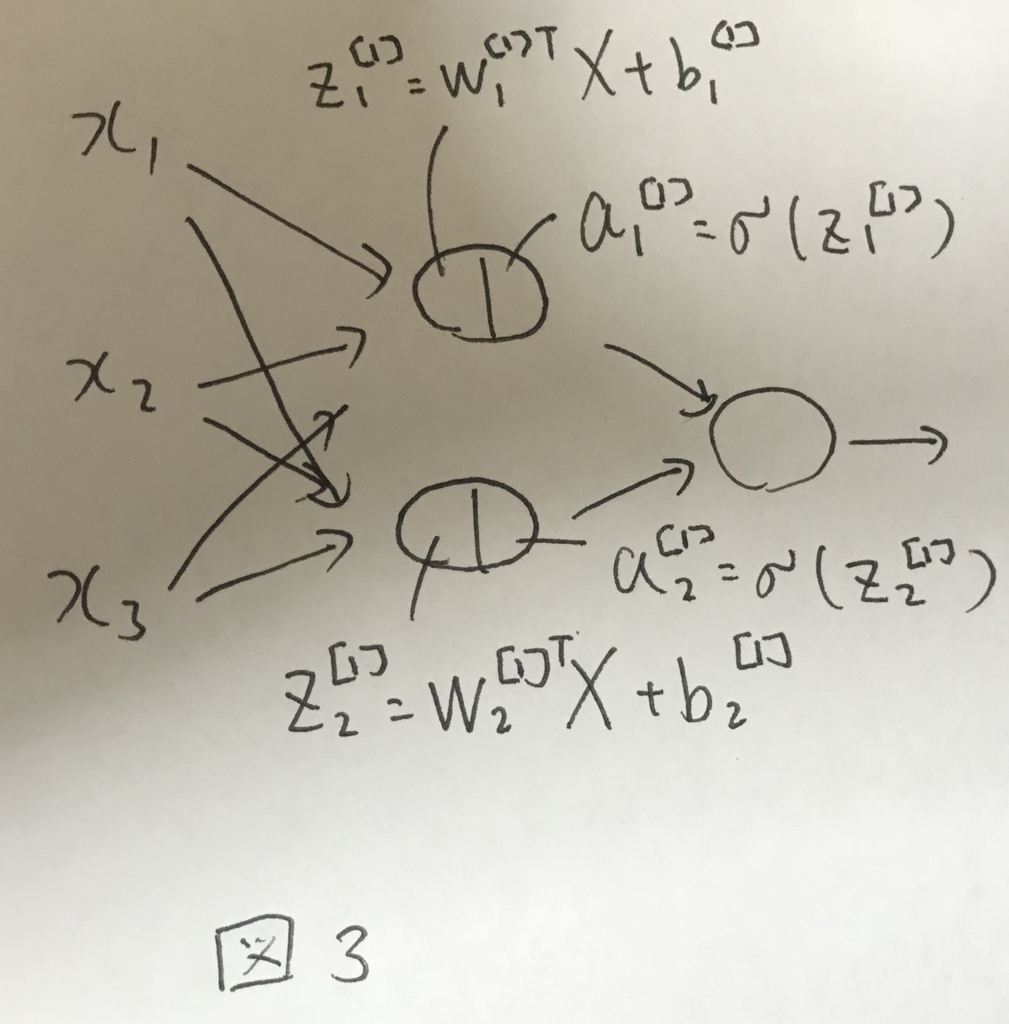
前の章でもあったように,ニューラルネットワークを実装する上では,ベクトル化が重要になる.
図3の処理を2層目にも適用し,ベクトル化すると図4のように表せる.
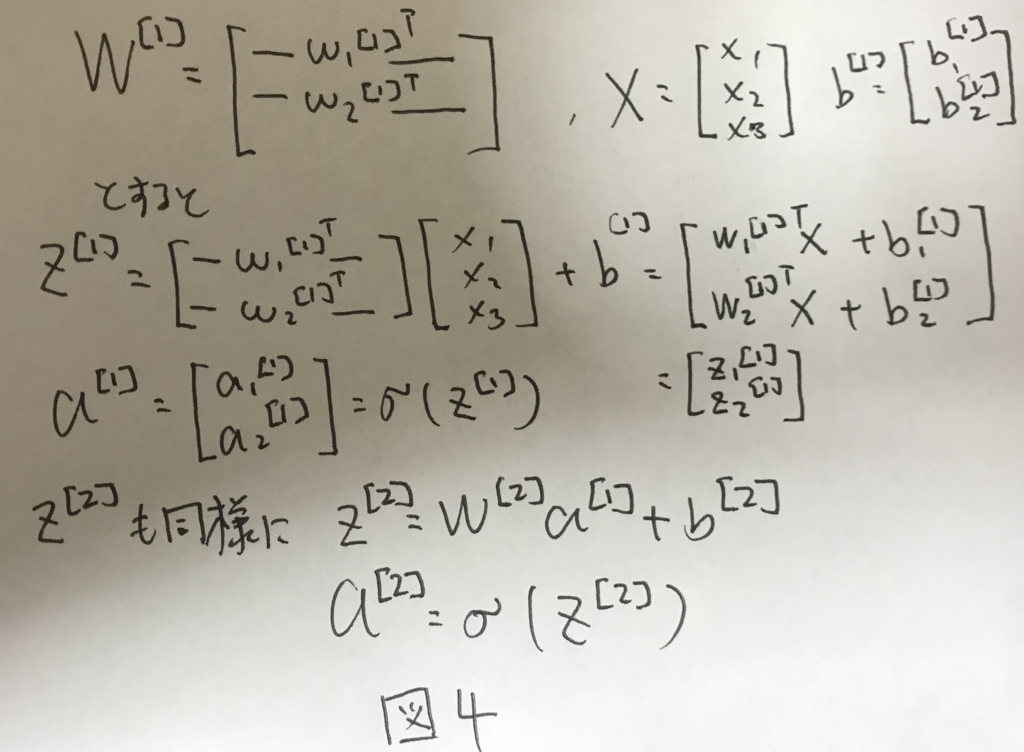
Vectorizeing across multiple examples
図4をさらに,トレーニングサンプルについて拡張してベクトル化すると図5のように表せる.

Explanation for Vectorized Implementation
これまでの振り返りなので割愛.
Activation functions
活性化関数についてのお話. これまではシグモイド関数だった部分について,ほかの選択肢として図6に示す3つがあげられた.
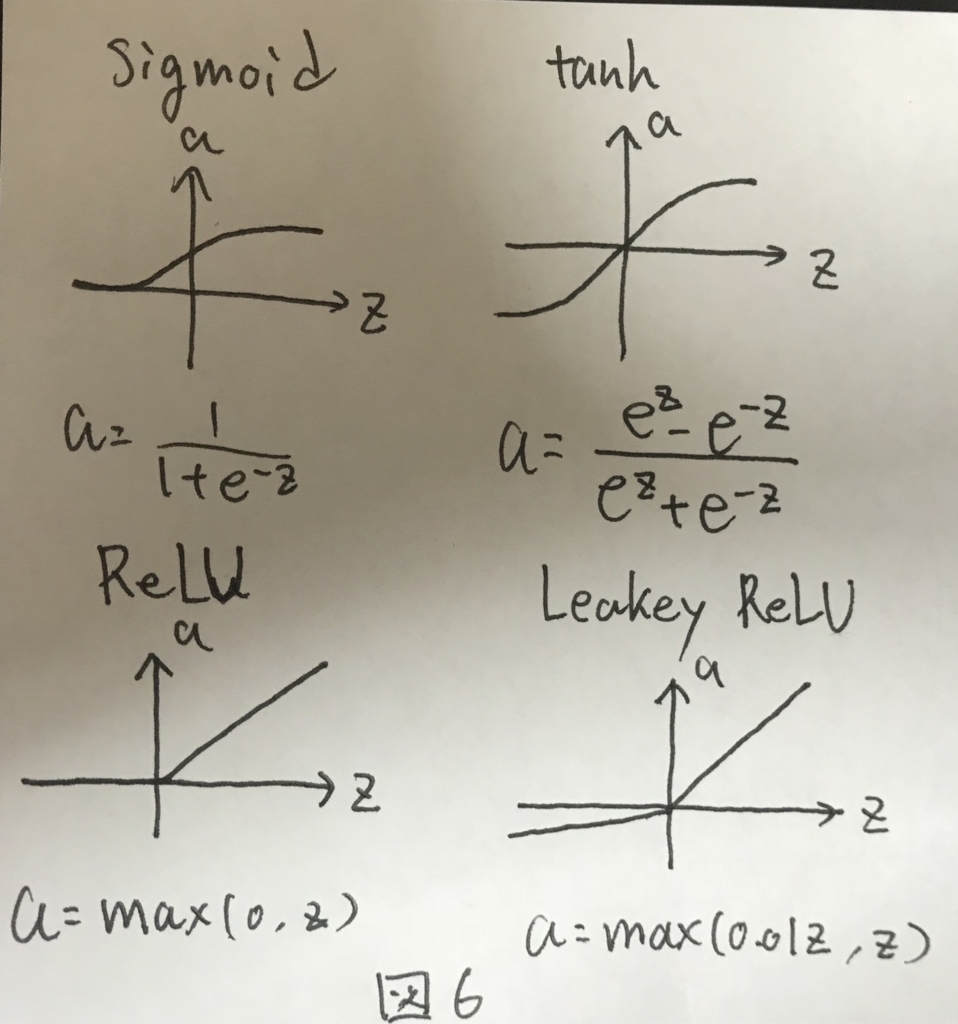
シグモイド関数は限られた用途のニューラルネットワークでしか用いられない. 代わりにtanhもしくはReLU関数が用いられる.
特にReLU関数はおすすめで,とある問題を解決することができる. とある問題とは,ニューラルネットワークにて最急勾配法を行う際に,活性化関数の微分した形が必要になる際に,引数Zの値が大きくなりすぎることで発生する問題であり,これが発生すると学習の効率が著しく下がる.
引数Zの値が大きくなると,tanhやsigmoid関数の場合,勾配がほぼ0となり,その結果として学習が全く進まないからである.
ReLU関数はZがどれだけ大きくなったとしても勾配は常に一定であり,上記の問題が発生しないという特性がある.そのため,ReLU関数は活性化関数としてよく用いられる.
なお,これまで見てきた4つの関数はいずれも非線形な関数であり,線形な関数は基本的に活性化関数として向かない.その理由は次の章で説明する.
Why do you need non-linear activation functions
図5において,A^[i]を求める際に用いる関数が例えばf(z)=zだったとする(線形関数). すると,図7のように,最終的に1層のニューラルネットワークとして表す値の組み合わせを見つけることができる.
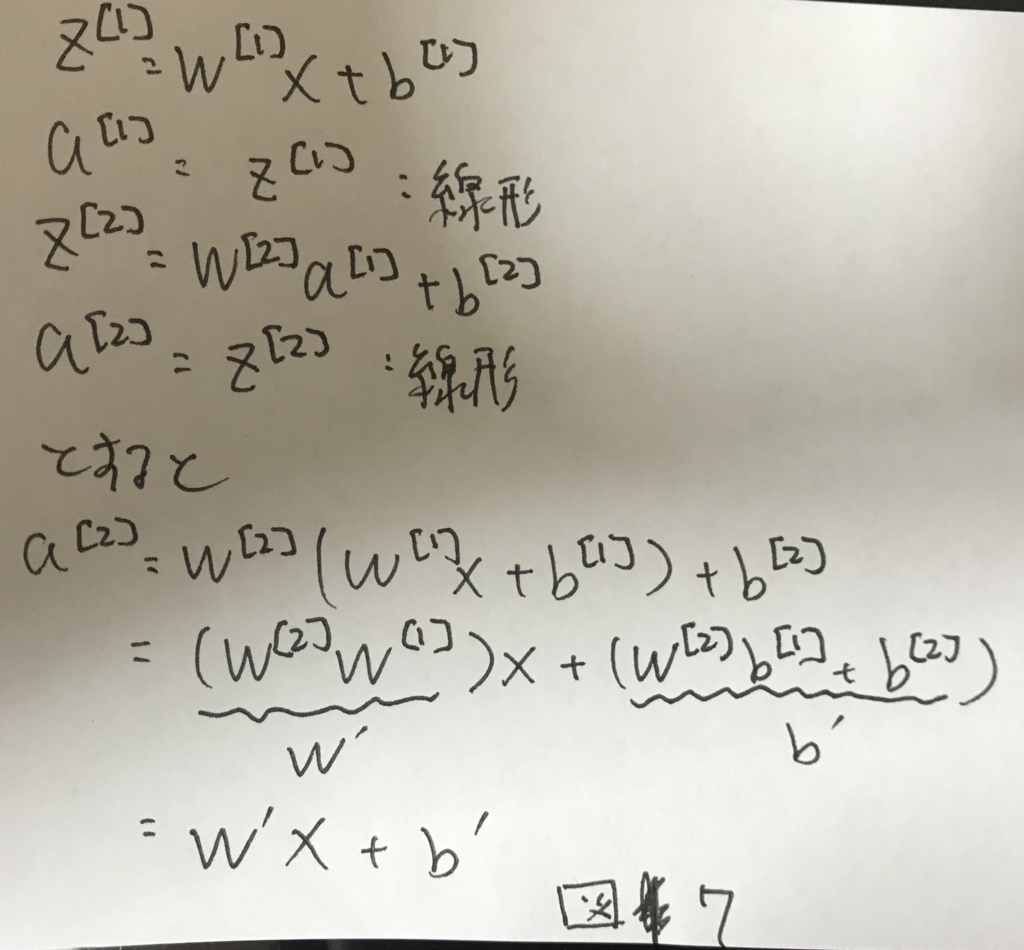
これは如何に多段にしても変わることはなく,何層にしたところで,線形関数を用いている以上は最終的には1ノードで表すことができる. そのため,表現力の高いモデルにはならず,多段にする意味がない.
これを避けるために非線形な関数を活性化関数として採用しなくてはいけない.
Derivatives of activation functions
次の章で詳細は述べるが,最急勾配法を行うためには活性化関数の微分形が必要になる. 各活性化関数の微分形を図8に示す.

Gradient descent for Neural Networks
計算グラフから,ニューラルネットワークでの最急勾配法を定式化する. まず,解きたい問題のアルゴリズムを図9に示す.

これを計算グラフを使って表すと図10のように定式化できる.
なお,np.sum(A, axis=1, keepdims=True)は,Aを縦方向にsumして,得られる解の形を(n,1)とするためのもの.keepdimsがないと,pythonの仕様から,(n,)という形状で返って来てしまうので扱いにくくなる.型を揃えるためのおまじないみたいなもの.

ここまで,図5では2層ニューラルネットの順伝播による推定を,図10では2層ニューラルネットの逆伝播による学習を定式化した.
これで,2層のニューラルネットの学習並びに推定において必要なことはほぼ出揃った.
次章では細かいことだが,重要な各パラメータの初期化について述べる.
Random Initialization
2層ニューラルネットワークではパラメータがw1,b1,w2,b2と4つあった. このうち,b1,b2については初期化時に考慮しなければならない特別な問題はないので,一般的には全て0で初期化される.
一方で,W1,W2については初期化時にそれぞれの要素をランダムで小さい値で初期化する必要がある.
初期化時にランダムな値ではなく,全て0で初期化すると,各レイヤーにおいて,ノード同士の出力の値が等しくなる.順伝播を繰り返し,誤差を計算して逆伝播する際に,出力が各レイヤー内部のノード同士で等しかったので,等しい値で学習が行なわれる. どれだけ学習を繰り返したところで,各レイヤー間の各ノードの値同士が等しい状況は変わらず,学習がうまくいかない. この問題を対称性の破れという.
これを避けるために,それぞれノードの初期値はランダムで初期化してあげる必要がある.
さらに,初期化の値を大きくした場合,活性化関数としてシグモイド関数やtanh関数を用いた場合,微分形の値がほぼ0になるため,学習が進まない.
そのため,各初期値は十分小さい値でランダムに初期化する必要がある.