Foundations of Convolutional Neural Networks
CouseraのDeepLearningのコースを受けている際の講義メモ.
https://www.coursera.org/learn/convolutional-neural-networks/home/week/1
今週はConvolutional Neural Networksということで画像の処理なんかによく使われるCNNのお話.
Coumputer Vision
コンピュータビジョンはDeepLearningによってかなり大きく進展した分野. 画像に写っているものを識別するような画像認識,画像から物体がどこにあるかを検知する物体検知,ある画像を別の画像のスタイルに変換するNeural Style Transferと言ったタスクがある.
画像は大変大量の情報を持つため,通常のニューラルネットを用いようとするととても大きなInputになる.これは計算コストの増大やOverfittingのリスクなどを引き起こす. CNNはこの問題に対してアプローチしている.
Edge Detection Example
CNNの前に,画像処理の分野でよく行われる,エッジ検知を見ていこう.
所望の画像に対して,特定のフィルタをかけると,どこにエッジがあるかを検出することができる. フィルタをかける処理のことを畳み込みと呼ぶ.
縦方向のエッジを検知するためのフィルタと,そのフィルタによってエッジが検知されている例を図1に示す.
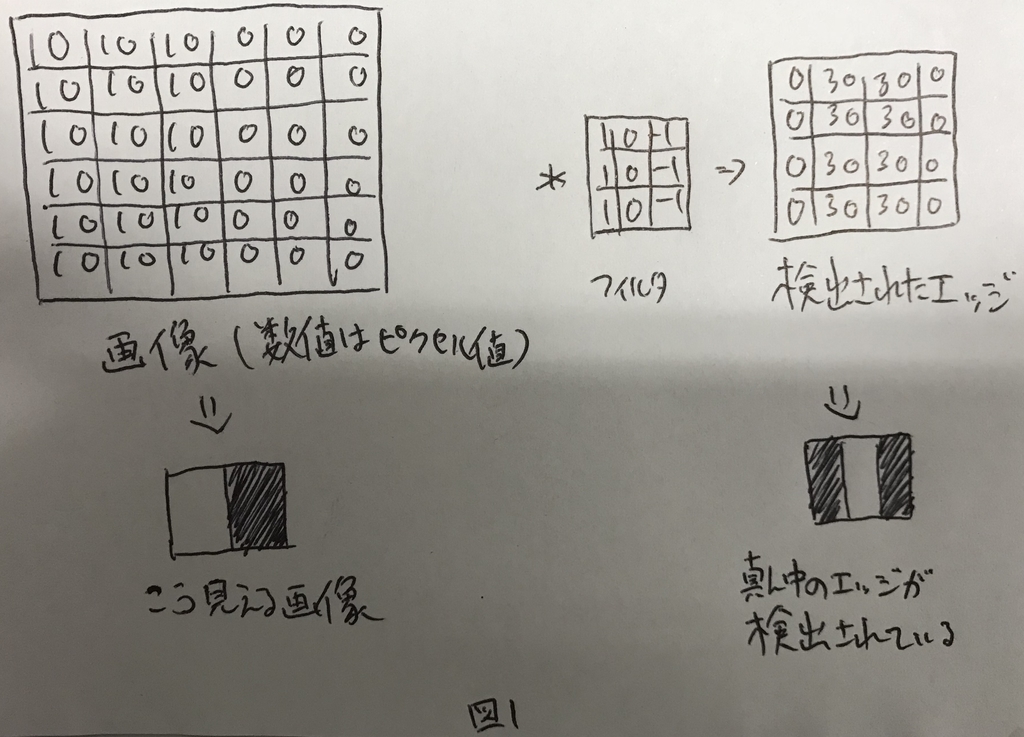
More Edge Detection
縦方向のエッジだけでなく,フィルタの形によってはいろんなエッジを検出できる.
例えば図2のフィルタでは横方向のエッジを検出することが可能.
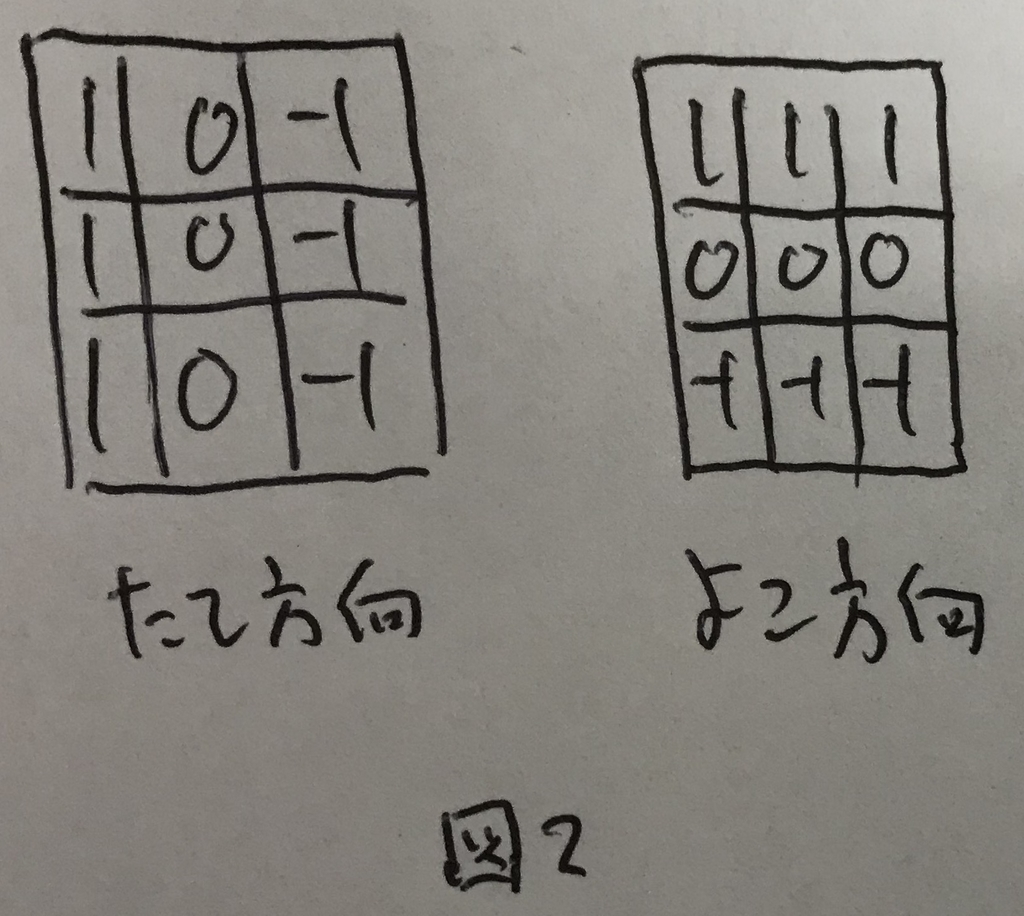
このように,フィルタの形によって検出できる特徴は異なる.
CNNでは,フィルタの各値をパラメータとして,画像の情報をよりよく表せるように学習を行う.
Padding
図1の例のように,畳み込みを行うと,画像が縮退する. フィルタをたくさんかけると画像がどんどんどんどん小さくなってしまう. これをコントロールするために,Paddingという技術がある. また,畳み込みを行う際に,左上のピクセルは畳み込みの計算時に1度しか活用されないが,中央のピクセルはフィルタの大きさ分だけ活用されるということもあり,画像の端っこの情報がうまく活用できていない.これもPaddingによって解決できる.
Paddingとは,畳み込みを行う前に,元の画像の淵にピクセルを埋めてしまうことを示す. 元の画像の外堀にPadding量の分だけピクセルを追加してあげる.この時,ピクセル値は0にするのが一般的.Paddingのイメージを図3に示す.
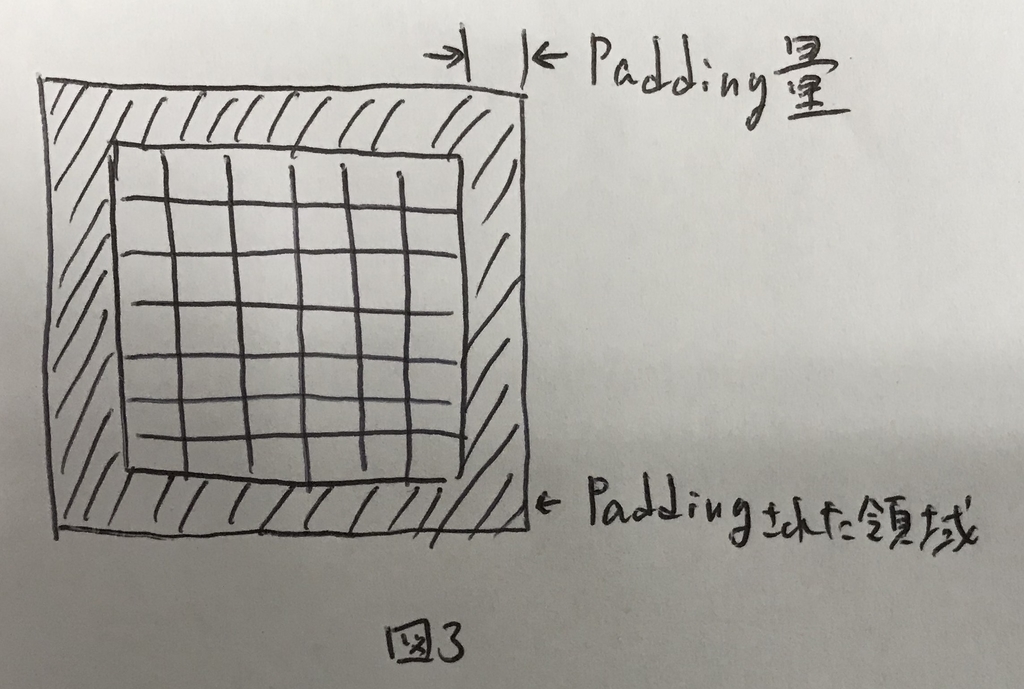
図3の斜線部分がPaddingで0埋めされた領域であり,どのくらい埋めるかはPadding量で決まる. Padding量が1だったら上下左右に1ピクセル追加するし,2だったら2ピクセル追加する.
Pagging量が0の場合をValidパディングと呼び,Padding量が「Paddingした結果,フィルタを畳み込んだ際に得られる画像の大きさが畳み込み前と変わらない」場合をSameパディングと呼ぶ.
なおパディング量をpと表記する.
Strided Convolutions
これまで,畳み込みは元の画像に対してフィルタを1つずつずらして行う想定で進めてきた. 実際には,これを1つではなく,2とか3とかずらすこともある.
このずらす幅のことをストライドと呼ぶ.
ストライドをsと表記した時,畳み込み後に得られる画像の大きさは,パディング量pを用いて図4で表せる.
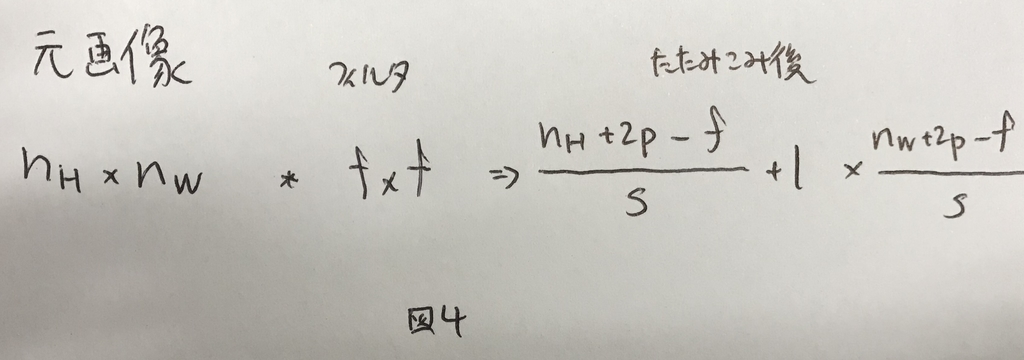
なお,畳み込み後のサイズは整数にならないケースもある.その場合は切り捨てる.
つまり,ストライドsで大きさfのフィルタをかけていき,もしもパディング量pでパディングされた画像からフィルタがはみ出す場合は計算を行わずに次に行くというようなフィルタのかけ方を行う.
Convolutions Over Volume
今までは2Dの例を見てきた. 画像を扱う際には,カラーチャネルがあるのでカラーチャネル(R/G/B)を含めた3D(縦×横×チャネル)の例を見て行く.
3Dの場合,畳み込みするフィルタも同じチャネル数が必要になる. 畳み込みは全てのチャネルについて透過的に実施され,最終的に得られるのは1チャネルの結果となる.
つまり,図5のようなイメージになる.
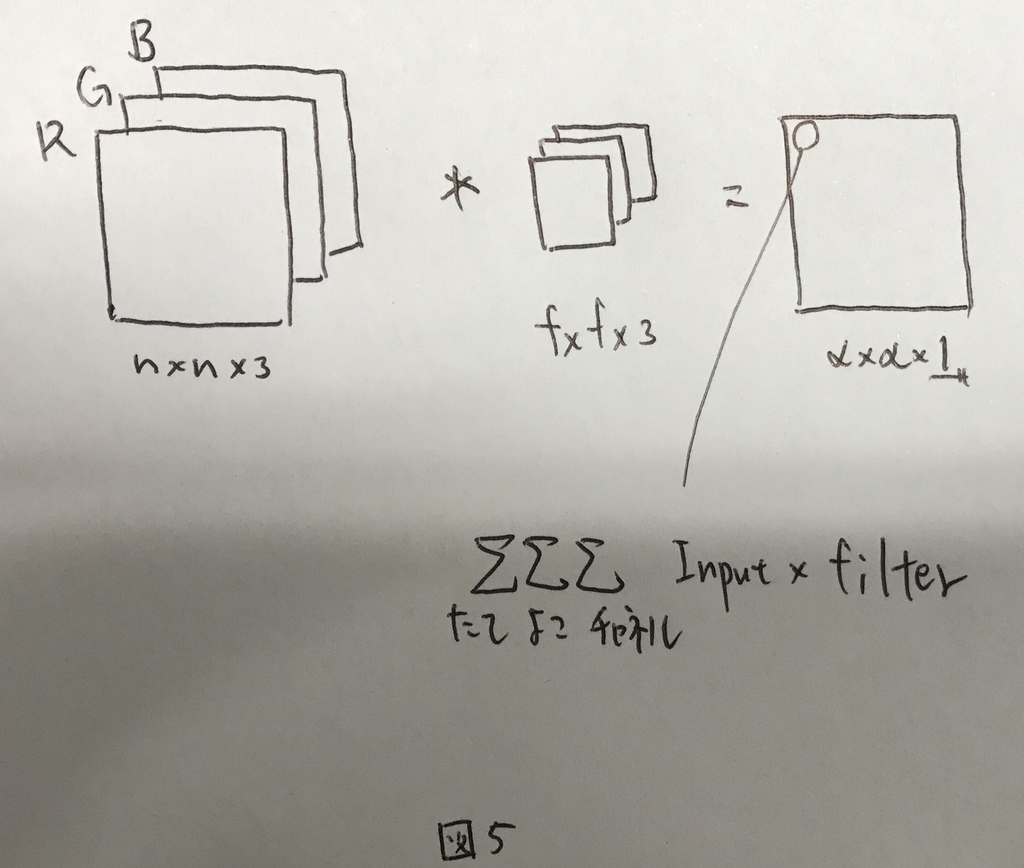
さらに,フィルタを複数かける例を考えると,図6のように最終的な出力も3D(たて×よこ×フィルタ数)になる.
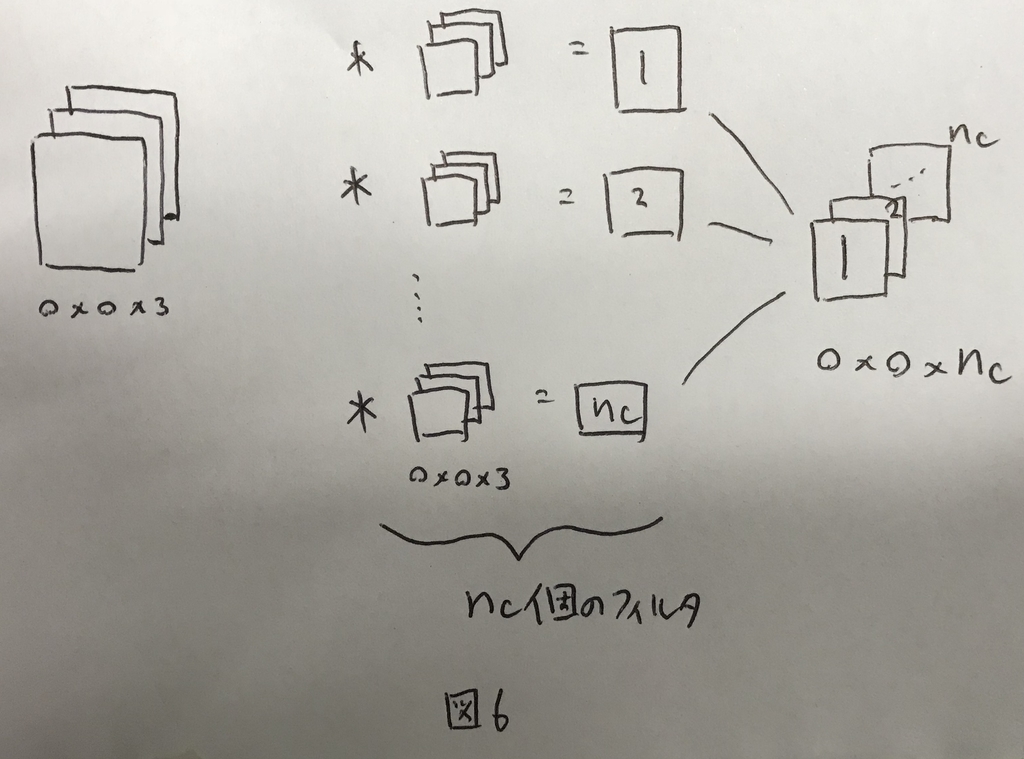
この,フィルタ数(nC)のことを,チャネル数と呼ぶことにする.
One Layer of a Convolutional Network
CNNの1レイヤーサンプルを図7に示す.
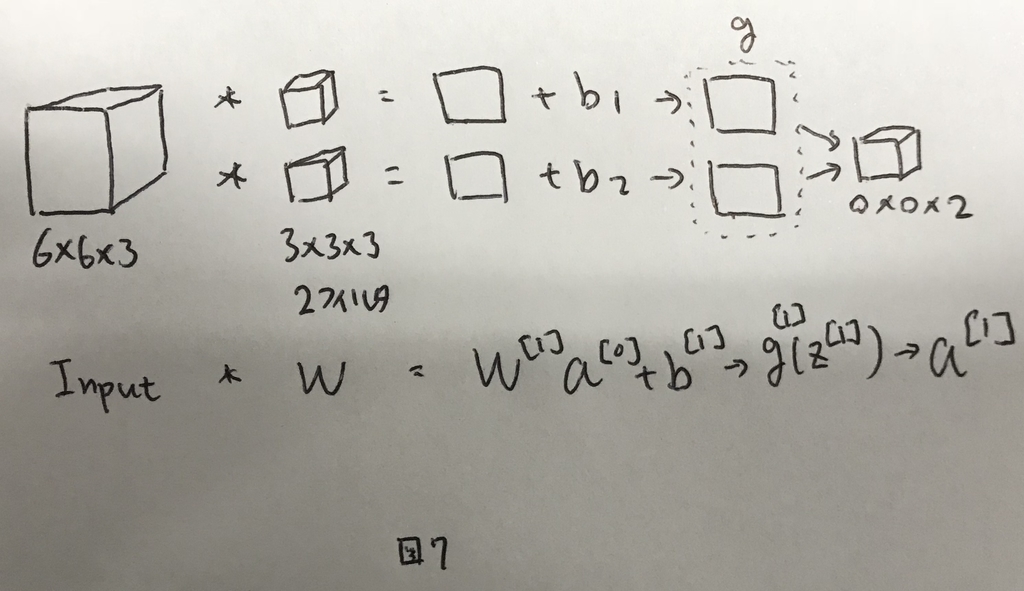
ここで,学習対象となるパラメタの個数は,Wの総数(3×3×3)とバイアス1を足した28個になる. さらにフィルタが2個だとすると,それぞれにバイアスが必要なので,28×2の56個が総数である. これらのフィルタを画像の全ての部分に共通して使って行く.後述するが,この特徴によりCNNは比較的学習対象のパラメータが少なく,過学習を起こしにくいという特徴がある.
CNNで用いる表記を図8にまとめる.
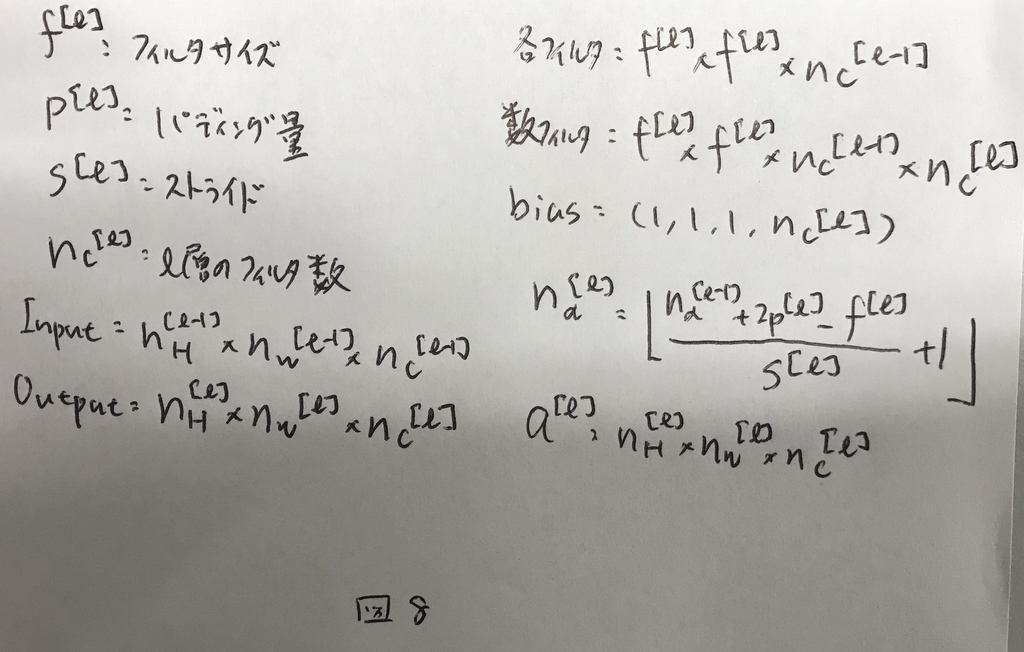
Simple Convolutional Network Example
CNNでは,3つのレイヤーを組み合わせることができる.
- 畳み込み層
- プーリング層
- 総結合層
Pooling Layers
プーリング層では計算量を減らすことと,特徴量をロバストにすることの2つが実現できる. プーリングには最大プーリングと平均プーリングの2つがある.
最大プーリングの計算イメージを図9に示す.
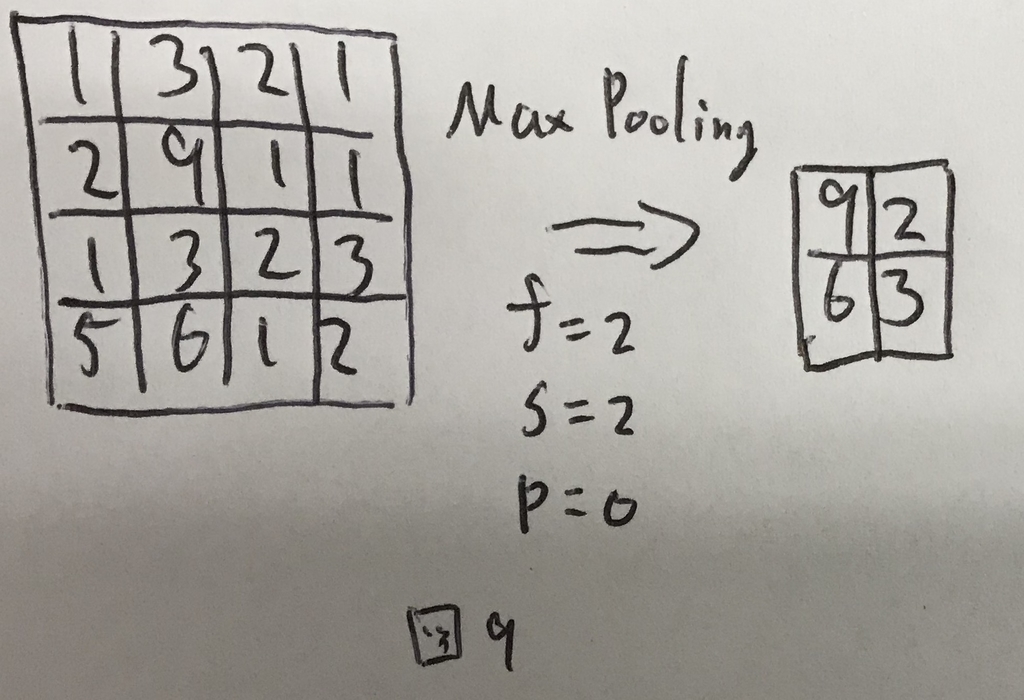
このように,フィルタ範囲内の最大値を返すものが最大プーリングである. 最大値を返すフィルタなので,学習するべきパラメータを持たないという特徴がある.
平均プーリングは,その名前の通り,平均値を返す.
プーリングはチャネルごとに計算され,チャネル数方向への縮退は起こらない.
Maxプーリングは実用的に効果が確認されており,よく使われる技術である.
CNN Example
これまで見てきたものをまとめて,CNNのサンプルを図10に示す.
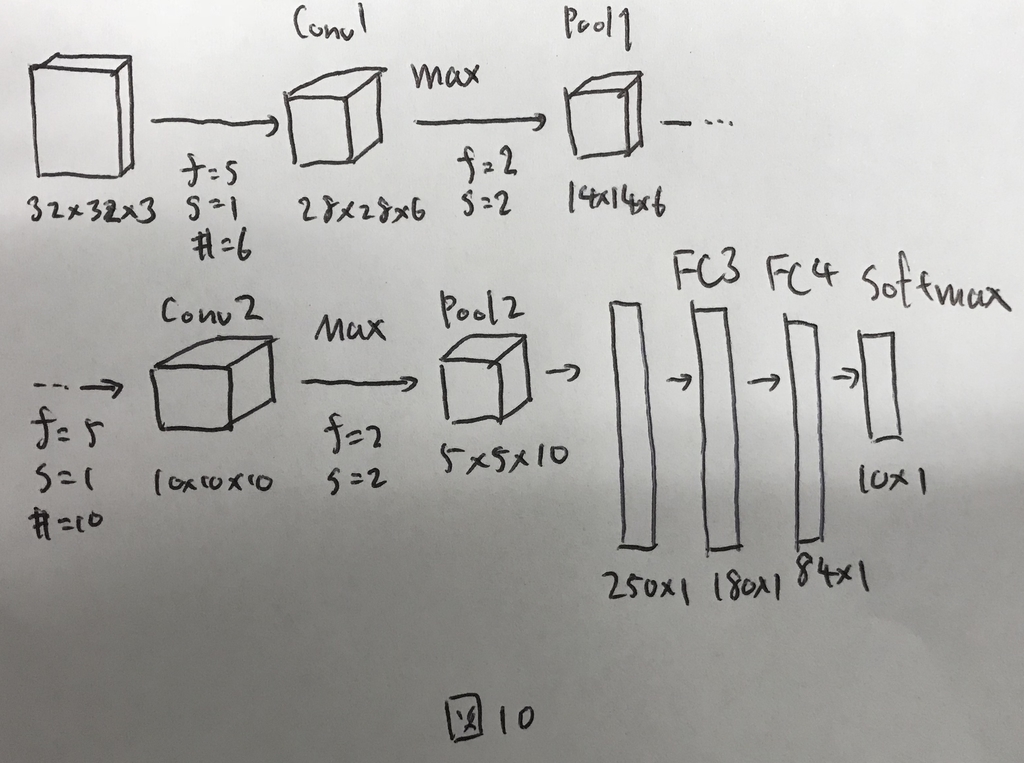
ここで,レイヤーの数え方には2つの流派がある. まず一つ目は,畳み込み層やプーリング層をそれぞれ1レイヤーとして数える方法である. もう一つ目は,学習すべきパラメータを持つもののみをレイヤーとして数える方法で,その場合はプーリング層はカウントしない. 本講座では後者の数え方を採用している.
図10のように,CNNでは設定すべきHyperparameterが無数にある. アプリケーションを構築する上では,一から構造を考えるのではなく,論文などで研究者がうまくやっている方法を参考にして活用することがおすすめ. 一般的なガイドラインとしては,nHとnWは少しづつ小さくするように設定し,nCは少しづつ増えるように設定して行くと良い.最後に総結合層を持ってきて,結果をえるように設計する.
Why Convolutions?
CNNの利点は大きく2つ. パラメータ共有とスパース結合という特徴である.これらがあるので,過学習しにくく,計算コストも低い.
パラメータ共有
パラメータ共有とは,画像の全領域に共有した同じフィルタを適用するということである. 32×32×3の画像にフィルタをかけて,28×28×6に変換する処理を考える. CNNでは,フィルタはf=5でフィルタ数は6で良いので,バイアス合わせて156個の値からなる. これが通常のNNだと32×32×3×28×28×6+1個の値からなるフィルタが必要であり,とてもじゃないが計算しきれない.
画像の処理などは特に,エッジ検出など基本構造を検出するためのフィルタは,画像の一部だけでなく全体で有用であるという特徴があるため成り立っている.
スパース結合
とある層のとあるピクセルは,直前の層の一部のピクセルとしか結合していないということをスパース結合であるという. 図11のように,とある層は直前の全ての層の計算結果ではなく,一部の層の計算結果からのみなる.
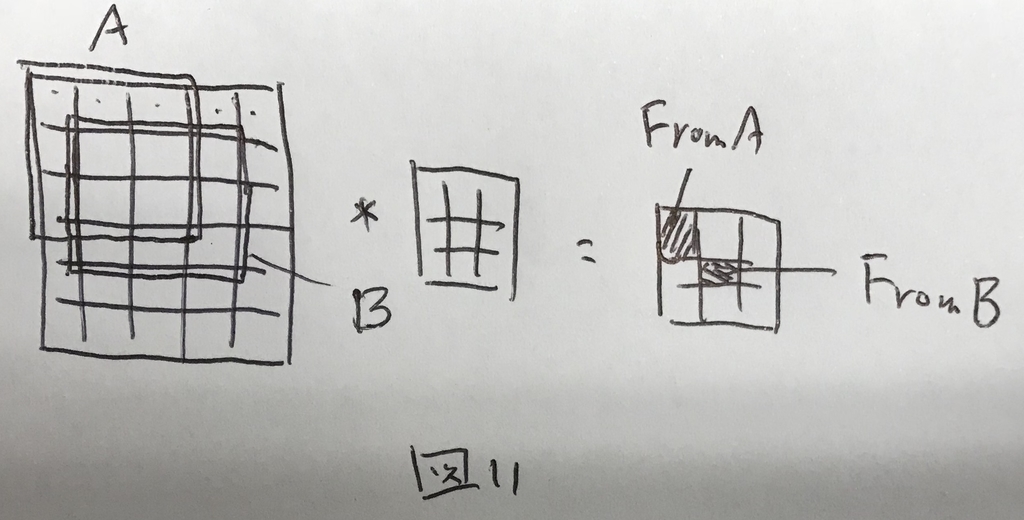
これにより,計算コストが少なく,過学習を起こしにくいという特徴が生じる.
SCDVについて学んだ
文章を数学的に扱いやすい形に変える方法の一つであるSCDVについて学んだ。
SCDVとは
ドキュメントを数学的に扱うことのできるような形に変換する方法のひとつで、Sparse Composite Document Vectorのこと。 他の方法に比べて変換後の形が小さくて扱いやすかったり、変換後の値を文章分類などに扱った際に精度が高いといった利点がある。
アルゴリズム
3つのパートに別れる。
Word Vector Clustering
まず、あつめてきたドキュメントから、単語を抜き出して、ボキャブラリセットを作る。
このとき、ボキャブラリセットには
~
の単語が含まれる。
これらについて、SGNS]によるWord2Vecを行い、各単語~
についての単語ベクトル
を求める。ここで、ベクトルの長さを
とする。
さらに、これらをガウス混合モデルを用いて、K個のクラスタに分類する。 Kをいくつにするかは任意で、SCDVのパラメータになっている。
分類した各クラスタについて、各単語モデル
がクラスタ
に所属する確率
を、全ての単語・全てのクラスタについて計算する。
Document Topic-Vector Formation
単語ベクトル~
に、各単語モデル
がクラスタ
に所属する確率
を掛け合わせたものを、単語-クラスタベクトル
と呼ぶ。
単語-クラスタベクトルを、すべてのクラスタ(k=1...K)について並べた行列を考える。
]
これに、という値(ドキュメント内部で単語
がどれだけ珍しいかを表す数値)を掛け合わせたものを単語-トピックモデル
と呼ぶ。
]× IFD(w_i)
なお、は
の行列である(長さ
のベクトルを
個横に並べて、実数を掛け算しただけなので)。
このを、特定のドキュメント
に出てくる単語の分だけ足し合わせた値を文章ベクトル
と呼ぶ
Sparse Document Vecotrs
得られたをスパース(ほとんどの要素が0で、残り数少ない要素のみが値を持つ状態)にするために、閾値を下回る要素については0に値を変換する。
こうして得られたものを、SCDVによる文章ベクトルとよぶ。
さいごに
このベクトルを用いて、文章分類などを行うと、他の方法に比べて精度がよい。
ML Strategy(2)
CouseraのDeepLearningのコースの受講メモ.
機械学習プロジェクトを進めて行くための戦略についてpart2.
Error Analysis
エラーを手動で分析してより良いモデルに育てて行くための知見をえる.
Carring out error analysis
モデルの能力が,人の能力に届かない範囲では,手動によるエラー分析が有効. モデルが分類に失敗したものを人がチェックして,どんな時に失敗しているかを分析する.
例えば,猫画像判定のアプリを考える.
猫画像判定システムの精度が90%あり,10%のエラーが残っているとする. エラーの中から1つの画像を見てみると,犬の画像を猫として判定していた. 犬の画像を大量に教師データとして取り入れると,この問題は解決できる可能性があるが,この問題に時間をかけることが有意義かどうか?
これに答えるのがErrorAnalysisである.
誤判定した中から,100サンプル程度ランダムに取り出して,その中に犬の画像がどれくらい含まれているかを見てみる.その結果,100個中2個であれば,これを改善したとしてもあまり効果はない. 100個中80個が犬であればこれを解決することはモデルの精度向上に大きな影響を及ぼすだろう.
このように,取り組むべき問題がクリアできた時,最大でどの程度精度が改善するか?といった指標をceilingと表現する.
Cleaning up incorrectly labeled data
全てのラベルが正しいわけではない.ラベルづけにミスっているケースもある. ラベルにミスが含まれていることがわかった時,これを付け直すか?という問題.
基本的に,DeepLearningなどのアルゴリズムは,ランダムなトレーニングセットのエラーに対しては堅牢なので,あまり気にする必要はない.エラー率があまりにも大きくて,データ数が少ないような場合は問題になるが,十分なデータがあり,許容できるエラー率であればモデルの精度に大きな影響はない.
Dev/TestセットにおけるエラーについてはErrorAnalysisをしてその影響を確認できる. 例えば,モデルの精度が90%でエラー率が10%のモデルについて,ラベルミスが0.6%であればそれは問題ないと言える. もしもこれが,モデルの精度が98%でエラー率が2%の状態で,ラベルミスが0.6%あると,問題になるケースがある. パラメータチューニングの際に,A(誤差率2.1%)とB(誤差率1.9%)の比較をしてどちらを採用するか決めなくてはいけないが,この際に,ラベルミスが0.6%あると,どちらがより良いパラメータなのかということを正しく判断できなくなるためである.
この場合は,Dev/Test双方のラベルづけを再度行う必要がある. なお,Dev/Testは同じ源からデータを得たいので,ラベルを修正するのであれば双方について同時に行うこと.
Build your first system quickly, then iterate
MLシステムを作る上では,まず簡単に作って,ブラッシュアップして行くような進め方が良い. まず,簡単に作って,その後にDev/Testセットを作ってメトリクスを決め,Bias/Variance AnalysisとErrorAnalysisを行って次に行うべき方向性を決める.
Mismatched traiging and dev/test set
Training and testing on different distributions
実際にシステムを動作させる環境から得られるインプットの他にも,例えば画像認識などのタスクであればネット上から画像をダウンロードしてきてそれを教師データとして活用することも可能になる.
その場合に教師データとDev/Testデータをどのように作って行ったら良いかというお話.
全部混ぜて,そこから教師データとDevデータとTestデータに分けるような方法はあまりよろしくない. 特にDevデータとTestデータはパラメータチューニングの際の意思決定に使われるものなので,可能な限り実環境で得られるデータに近しい必要がある.
なので,まずは必要なだけのDevデータとTestデータを可能な限り実環境から得られるデータで構成してしまう.そしてあまりのデータとネットから落としてきたデータを一緒に教師データとして扱うといった方法が良い.Dev/Testはあくまで同じ源から得られるようにしたいので注意.
Bias and Variance with mismatched data distributions
Bias/Variance Analysisを行う際に,データソースの違いが気になる.
例えば,HumanLevelのエラー率が0%だとして,TrainingErrorが1%でDevErrorが10%のシステムがあるとする. 一見するとHighVarinaceの問題のようにも見えるが,TrainingSetとDevSetが別の情報源からきているとすると,その影響がどの程度なのか?という疑問が持ち上がる.
これを解決するために,新たに「Training-Dev」というデータセットを作成する. これは,Trainingセットと同じ源から得られたデータのうち,学習には使われないデータのこと. Trainingセットを作った後で,そこからランダムに一部のデータをTraining-Devセットとしてあげると良い.
TraingErrorが1%でTraining-DevErrorが9%でDevErrorが10%だとすると,これはHigh Varianceの問題である.
TraingErrorが1%でTraining-DevErrorが1.5%でDevErrorが10%だとすると,これはデータミスマッチの問題である.
TraingErrorが10%でTraining-DevErrorが11%でDevErrorが12%だとすると,これはHigh Biasの問題である.
TraingErrorが10%でTraining-DevErrorが11%でDevErrorが20%だとすると,これはHigh BiasでかつHigh Varianceな問題である.
Addressing data mismatch
データミスマッチの問題にどうアプローチしていくか,確実な方法はないが,試すべき方法はある.
まずはErrorAnalysisを行って,TraingデータとDevデータの違いを探してみる. 例えばDevデータはよりノイズが強いとかそんな情報がわかるとよい.
これがわかったら,TrainingデータをよりDevデータに近づけるための努力を行う. いくつか方法はあるが,例えばDevデータと同じ環境でデータを大量に確保するとか,データ合成を行って擬似的にTrainingデータをDevデータに近づけるなどする.
データの確保は難しいケースが多いので,データ合成は手軽に試せるのでおすすめ.
データ合成する際には,合成するデータのバリエーションに注意が必要で,バリエーションが少ないとoverfittingを引き起こしてしまうリスクがある点に注意すること.
Learning from multiple tasks
Transfer learning
転移学習について.
同一のインプットを受けて,異なるタスクを行うモデルを効率よく学習するための仕組みとして転移学習は有効.
例えば,画像をインプットに,猫を判別するようなタスクがあったとする. このために,画像を大量にインプットし,モデルを学習する. この学習したモデルの浅い層は画像のエッジを検出したり,平面を検出したりといったプリミティブな表現を獲得している.深い層ではこれを活用して猫の顔を認識するような動きになる.
このモデルを,例えば画像をインプットに骨折しているかどうかを判定するようなタスクに応用することができる. 浅い層はそのまま用いて,深い層を再度学習させることで,骨折を判定させるモデルに転移する.
骨折診断するための画像郡であっても,猫の画像を判定するための画像郡であっても,画像としてのプリミティブな特徴は変わらないことから,こんなことができるわけである.
はじめに,浅い層を学習する過程をpre-trainingと呼ぶ. 次に深い層を学習させる過程をFineTuningと呼ぶ.
転移学習は以下の条件の時に効果を発揮する.
- タスクAとタスクBが同じinputを持つこと(双方画像であるとか)
- タスクBよりタスクAのデータが大量に存在していること.Aが少ないとあまり効果がない
- タスクAの学習で得られた低レイヤーの特徴がタスクBにおいて有用であること
Multi-task learning
複数のタスクを同時に行うモデル. 車載カメラにおいて,「歩行者を検知する」「標識を検知する」と言ったタスクを,それぞれ個別のモデルではなくまとめて1つのモデルで行うようなイメージ.
こうすることで低レイヤーを共通して使いまわせるため,効率が良い. 4つのタスクを1つのモデルで実現したいとした時,教師データの正解データとして,必ずしも各教師全てに4つの判定結果が入っている必要はない.
「歩行者の検知」「標識の検知」「信号の検知」「別の車の検知」の4タスクを実施したいとして,とある教師データの正解が「歩行者の検知:yes」「標識の検知:no」「信号の検知:?」「別の車の検知:?」と言ったようにデータに欠損が生じていた場合は,?については無視してあげれば良いので,学習に用いることは可能である.
Multi-task Learningは以下の条件の時に効果を発揮する.
- 低レイヤーが共通して使いまわせること
- 各タスクのデータ量が同じくらいであること
- 十分に大きなネットワークを学習させられること
実践的には,転移学習はたくさん使われているケースがあるが,Multi-taskLearningが使われるケースはあまりない.
End-to-end deep learning
What is end-to-end deep learning?
音声の自動書き起こしタスクを考える.
これまでの世界では,音声をまず,音声特徴に変換し,それをもとに音素を割り出し,さらにそこから単語を得てそれを元に書き起こし結果を得ると言ったpipeLineタスクを行っていた.
これを,直接音声の波形から書き起こし結果をえると言ったものがEnd-to-end DeepLearningである.
データ量が十分に大きい時にはこのアプローチが可能になる.データ量がそこまで大きくないときはEnd-to-endは難しいため,タスクの分割を検討する必要がある.
例えば,画像認識のよる入室管理システムのようなものを作る時,画像全体から特定の人が写っているかを識別するのはなかなか難しい. そこで,まずは顔がある場所を反転し,その顔がある場所の中から特定の人物かどうかを判定するようなタスクを行う.
こうすることで,困難な問題が2つのステップに分割される.
Whether to use end-to-end deep learning
End-to-endの利点と欠点は以下の通り.
利点
手作りの特徴量が不要であり,データを食わせればなんとかなる.
欠点
データが大量に必要になる. 機械学習のプロジェクトにおいて,手作りの特徴量をモデルに注入することは精度をあげるためにかなり有効なアプローチだが,End-to-endのアプローチではそれができない. データ量が十分にあれば手作りの特徴量は不要になるので問題ないが,データ量が得られないとこれが問題になる.
データ量はかなり大事な要素である.
ML Strategy (1)
この週と次の週では機械学習プロジェクトを進めていくための戦略について説明する.
Why ML Strategy
MLプロジェクトを進めていくための戦略がなせ必要なのか?
モデルの精度が例えば90%であるとした時,それをさらに改善するためにどんなことをしたらより改善できるのか?という判断を適切に行えることはプロジェクトの効率や進捗に大きく影響する.
そのため,この週と次の週で話される戦略を理解し,活用することが大切になる.
Orthogonalization
日本語でOrthogonalizeationは直交という意味. 機械学習プロジェクトにおけるモデルの調律時に意識すると良い考え方として「Orthogonalization」がある.
これは,1度に1つのものを変えてみるということ.
まず調律においては,はじめに「教師データによりよくフィットするように」という点に絞って調律を行う.次に「バリデーションセットによりよくフィットするように」という点に絞って調律を行う.
同時に双方を満たすように調整するのではなく,それぞれ独立して調律を行うことが効率的な進め方につながる.この考え方をorthogolanizationという.
Single number evaluation metric
調律を行う際には,例えば分類制度や処理時間など,複数の指標を最適化しようとして調律すると行った戦略が考えられるが,より効率的な調律を進めるためには,1つの調律するための指標を決めてそれを追い求めるほうが効率が良い.
どのように1つの指標を決めるかについては後ほどの授業で述べるが,例えばF1Scoreなどがある.
Satisficing and Optimizing metric
モデルのパラメータのセットから,最適なものを見つけたい. その際に,複数のメトリクスがあると意思決定が難しいことがある.
例えば,(F1Score,処理時間)がA(90%, 80ms),B(92%, 95ms),C(95%, 1500ms)だとする. この時, F1Scoreだけに着目すると最適なのはCだが,処理時間の観点に着目すると最適なのはBとなる.
さらにメトリクスが増えて,N個になった時,適切な判断を下すのは難しい.
これをうまく扱うための方法として「1つを最適化対象として,他のN-1は制約条件とする」という考え方がある.
例えば,F1Scoreを最適化対象として,処理時間は制約条件とするような考え方である. 「処理時間は100ms以下であること」という制約を課し,その条件下でF1Scoreを最適化するものが良いパラメータセットであると考える.
すると先ほどの例は処理時間が制約条件に収まり,F1Scoreが最適なBがベストな選択であると判断できる.
Train/dev/test distributions
特にDevセットとテストセットについては,同様の発生源からデータを得るようにすることが大切になる. トレーニングセットを使い,パラメータを決めて学習したモデルを,Devセットで評価して,最適なパラメータに調整していく.その際に,Devセットとテストセットがかけ離れていると,その調整が全く意味をなさなくなってしまう. これを避けるためにも,Devセットとテストセットは同一の発生源からデータを取得できるように心がけるほうがいい.
Size of the dev and test sets
データ総量がそんなに大きくなかったこれまでの世界では,教師データとして総量の60%を,Devセットとして20%,テストセットとして20%を使うようなバランスが多かった.
近年,扱えるデータ量の増加に伴って,母数が増えたので,総量の20%をDevとテストセットに使う必要は必ずしもなくなった. 最近では98%を教師データとして使い,残り1%づつをDevセットやテストセットとして扱うケースもある.
さらに,テストセットは最終的なシステムのパフォーマンスを推定するためのものであり,最終的なシステムのパフォーマンスの推定が不要であれば,テストセットを用意しないという選択もありうる.
When to change dev/test/ sets and metrics
メトリクスがモデルの「良さ」を直接的に反映していないことがわかったら,メトリクスを変更する必要がある.
例えば,誤差1%で動くがミスした際に大きな事故がつながるAモデルと,誤差5%で動きミスしたとしても事故には繋がらないBモデルがあるとする.
メトリクスを誤差率にすると,モデルAの方が良いように見えるが,実際には事故が起きると様々な損害につながるため,メトリクスとしては誤差率だけでなく,事故の大きさのようなものも含むべきである.
このようなことが後から判明したら,そのタイミングでメトリクス自体を変更する必要がある.
Why human-level performance?
機械学習によるタスクの精度は近年向上してきており,人の能力と戦えるレベルに進化してきた. 分野によっては人の能力を超えるような成果も出始めている.
機械学習の分野では,人の能力に比べてモデルの精度がどの程度か?という問いが,重要な指標として扱われている. 機械学習のモデルの到達可能な最大精度を見積もるために,人の能力が活用できるからである.
到達可能な理想的な最大精度に達した際に残る誤差をBayesOptimalErrorと呼ぶ. 人のパターン認識力や識別力はとても高く,BayesOptimalErrorと人間の限界値は近しい.
そのため,モデルが到達可能な精度として,人の識別能力がBayesOptimalErrorを間接的に示す指標として扱われるのである.
さらに,別の観点からは,人の能力限界までは,人が教師データを作成できるので,学習に用いる教師データを増やすことが容易いということや,人の能力限界までは,モデルがどのような条件の時に失敗しやすいかを人が理解できるので,最適化しやすいため,人の能力限界までモデルの精度をあげることは,それ以上に引き上げることに比べるとやりやすい.
そのため,図1のような投資する時間とモデルの精度の関係が描ける.

Avoidable bias
過去の章で,モデルの性能を評価する指標としてバイアスとバリアンスについて考えた. 過去の章で説明したバイアスとバリアンスはHumanLevelError(≒BayesOptimalError)が0であるとして計算したもので,実際は異なる.
バイアスは教師データについての誤差率から,HumanLevelError率を引いた値として定義される.バリアンスは,バリデーションセットデータについての誤差率から教師データについての誤差率を引いた値として定義される.
例えば,HumanLevelErrorが1%で,教師データに対する誤差率が8%,バリデーションセットデータに対する誤差率が10%だとすると,バイアスが7%でバリアンスが2%なので,Highバイアスな状態であると言える. これが,HumanLeverErrorが7.5%のような場合は,バイアスが0.5%でバリアンスが2%なので,Highバリアンスな状態であると言える.
このように,HumanLevelErrorは誤差率の分析を行う上でも重要な指標となっている.
Undrstanding human-level performance
HumanLevelErrorとは具体的にどうやって計算したら良いのか? 例えば以下のような状態を考える.
Task:画像による骨折診断 * 一般的な人の誤差率:1% * 一般的な専門家の誤差率0.5% * エキスパートな専門家の誤差率0.4% * エキスパートな専門家のチームによる誤差率0.3%
この場合は,BayesOptimalErrorはエキスパートな専門家チームによる誤差率0.3%よりも低いと見積もるのが正しい.
Supassing human-level performance
近年では,分野によっては人の能力を超えるような成果が出始めている.
広告配信やレコメンドシステムなど,構造化されたデータを扱うようなタスクの場合に,モデルが人を超えることが増えてきている. 人は構造化データの処理があまり得意ではなく,機械はそれが得意だからである.
構造化されていないような,画像認識や音声認識などの分野においては,一般的には人の能力を超えることは難しいが,近年は扱えるデータ量が増えてきたこともあり,少しずつ人の能力を超えるモデルが出てきている.なので,モデルが人を超えることは不可能ではないので,チャレンジする価値がある.
Improving your model performance
ここまでの内容をまとめて,モデルのパフォーマンスを向上させて行くためのプロジェクトの進め方ガイドラインを示す.
教師データにフィットさせる
まずは,モデルを十分に教師データにフィットさせることを考える. これは,バイアスを下げることを意味する.
モデルのネットワークを大きく,深くしたりする必要があるかもしれないし,学習期間をもっと伸ばす必要があるかもしれない.学習を効率良く進めるために最適化アルゴリズムを変える必要があるかもしれないし,CNNやRNNなど別のネットワークアーキテクチャを試すべきかもしれない.
バリデーションセットにフィットさせる
十分に教師データにフィットしたら,次はバリデーションセットにフィットさせる. つまり,バリアンスを下げる.
もっともっとたくさんの教師データを集めて学習させることでこれが達成できるかもしれない. 正則化(L2正則化やDropOut)することで解決できるかもしれないし,データを水増しするためにデータ拡張を行う必要があるかもしれない. CNNやRNNなど別のアーキテクチャを選択することで解決できるかもしれない.
この2つのステップを,一度に片方にだけ集中して行い,反復させることで効率良くモデルが育って行く.
Hyperparameter tuning, Batch Normalization and Programming Frameworks
CouseraのDeepLearningのコース2つめ最終週. 学習メモです.
Hyperparameter tuning
Tuning process
これまで見てきたように,チューニングするべきhyperparameterはいっぱいある. これをうまくチューニングするためのガイドラインを説明する.
チューニング対象
チューニングするべき対象は以下の通り.
- 学習率α
- Momentumのβ
- Adamのパラメータβ1とβ2
- Layer数
- 隠れユニット数
- 学習率減衰の係数
- ミニバッチサイズ
このうち,一番大切なチューニング対象は学習率αであり,積極的にチューニングを行う. 次に大事なのはMomentumのβと隠れユニット数,ミニバッチサイズである.これらもチューニングする. そのあとに大事なのがLayer数と学習率減衰の係数であり,これはあまりチューニングしない. 最後に,Adamのためのパラメータはほぼチューニングせずにデフォルトの値を用いることが多い.
チューニング方法
単純化するために2つのパラメータを考える.
従来のやり方では,例えばN回の施行ができるとすると,2つのパラメータから√N個ずつ候補を決め,それらをGrid的に全探索して良いものを最適な組み合わせとして使っていた. この方法では,各パラメータについて√N個のパターンを試すことしかできないため,実はあまり効率が良くなかった.
そこで,DeepLearningの世界では,Grid的な探索は行わず,ランダムにN個の候補をパラメータ空間から取り出して探索を行う.こうすることで,各パラメータに対してN個の値を施工することができ,効率が良くなる.
さらに,必要に応じて粗密サンプリングを行う. 粗密サンプリングとは,2つのステップからなるチューニング方法で,
- まずパラメータ空間の中で荒く候補点を決めて探索する
- 良い結果が得られたサンプル付近からさらに重点的に候補点を抽出し,改めて探索する
という方法である.
闇雲に全探索するより効率が良い.
Using an appropriate scale to pick hyperparameters
必ずしもリニアスケール上でランダムサンプリングすれば良いというわけではないというお話.
例えば隠れユニット数について,だいたい50-100の間くらいに正解があるだろうという状況であればリニアスケール上でランダムにサンプリングして探索すれば問題ない.
一方で,学習率αについて,0.0001から1くらいの間に正解があると思われるときに,リニアスケールでランダム抽出すると効率がよくない.
何も考えずにランダム抽出すると抽出される候補の割合が,0.0001~0.1が10%,0.1~1が90%になる. αのようなレンジの場合,そうではなく,0.0001~0.001と0.001~0.01と0.01~0.1と0.1~1の間のサンプルの割合を等しくしたい.そんな時はリニアスケールではなくログスケール上でのランダムサンプリングを行う必要があるので注意が必要.
Hyperparameters tuning in practice
実践的に効率的にチューニングをする方法について.
使える計算リソースによってチューニング方法を選択する必要がある. 選択肢は2つあり,「Baby sitting one Model」と「Parallel Model」である.
Baby sitting one Model
計算リソースが限られているケースで選択する. コスト関数を観察しながら,学習中にパラメータを手動で調整するようなモデル. 最初はランダムに初期化したパラメータを使い,学習を開始する. コスト関数の値を観察しながら,手動で学習率をあげたり,下げたりする.
このアプローチは別名パンダアプローチとも呼ぶ. パンダは子供が少なく,1人の子供を大切に育てるため. 手塩にかけてモデルを育てていくイメージ.
Parallel Model
潤沢に計算リソースを持っているケースで選択する. 複数のモデルを同時に別パラメータで学習させ,その中から一番良いものを選び出す方法.
前述のパンダアプローチに比べてキャビアアプローチというイメージ. チョウザメは一度に大量の子供を産むので,一人一人を大事に育てることはしない.
Parallel Modelも同様に,たくさん施工して良いものだけを選択する. Baby sitting one Modelのように1つに手をかけたりはしない.
Batch Normalization
バッチ正規化という方法について説明する. バッチ正規化はネットワークをロバストにすることができるため,hyperparameterのチューニングが楽になる.また,学習を高速化する効果も望める.かなり重要なアルゴリズムの1つ.
Normalizing activations in a network
以前,ロジスティック回帰において,Inputとなるベクトルを正規化することでモデルの学習が高速化されることを見てきた.
ニューラルネットワークはロジスティック回帰のノードを積み重ねたようなものであり,各ノードへの入力となる部分を正規化することで学習を早めることができるのではないだろうか,というのがバッチ正規化のアイディアとなる.
なお,実際には各ノードへの入力a=g(z)の正規化ではなく,zの正規化を行うほうが実践的によく用いられる手法であるため,zの正規化を行うものをバッチ正規化として説明する.
バッチ正規化は,ニューラルネットワークを学習する過程のなかで,各隠れ層について図1のような処理を行う.

ここでΓとβはそれぞれモデル学習時に学習するものであり,学習方法については後述する. ここで大切なのは,Zは一度平均0,分散1に正規化された後で,学習されたΓとβを用いて平均と分散が補正されているという点である.
この補正されたZを用いてニューラルネットワークの学習を進めることになる.
Fitting Batch Norm into a neural network
ニューラルネットワークの中にバッチ正規化を取り入れた全体像を説明する. バッチ正規化を取り入れる前のニューラルネットワークと取り入れた後の違いを図2に示す.
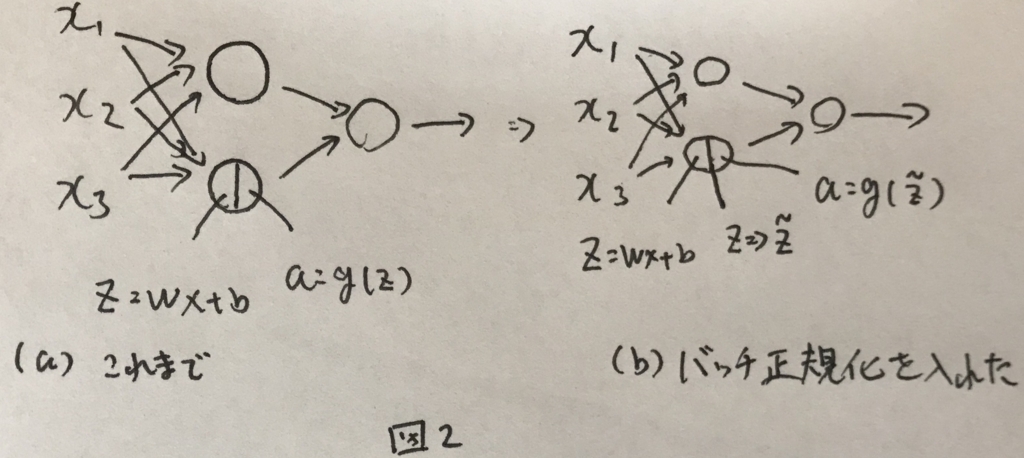
ざっくりこんなイメージ.
学習したいパラメータは図3のようになる.

ただし,バッチ正規化によって,Zは一度平均0で分散1の値に変換される. この変換において,平均が0に補正される際に,バイアス項bが0になる. なので,バッチ正規化時には,bはパラメータから意図的に外されなくてはいけない,
これを考慮して,正しい学習対象のパラメータは図4のようになる.
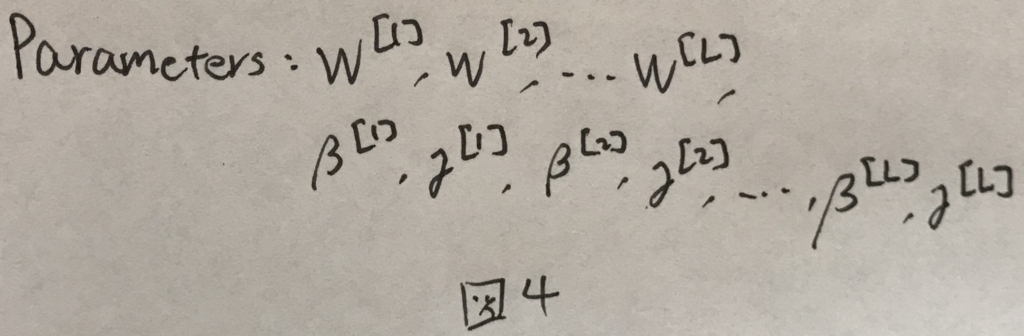
ミニバッチへの適用
ミニバッチ勾配法へバッチ正規化を適用する際には,平均と分散の計算をミニバッチに含まれるデータのみで毎回計算すること.一旦全ての教師データから平均と分散を計算して補正に用いるようなことはせず,あくまでミニバッチの中でのみ完結させる.
ミニバッチ勾配法へバッチ正規化を適用したアルゴリズム(1epoch)を図5に示す.

なおこれはスタンダードな勾配法だが,MomentumやRMSpropやAdamについても同様である.
Why does Batch Norm work?
バッチ正規化を行うことで,深い層が入力の変化についてロバストな耐性を得ることができるため,バッチ正規化は有効.
一方副作用もあり,ミニバッチサイズが小さい状態でバッチ正規化を行うと正則化と同様の効果が発生する.ミニバッチサイズを大きくしてバッチ正規化を行うことで正則化効果を下げることは可能.
Batch Norm at test time
学習したモデルを用いて予測を行う際には,1つの入力を処理して出力を得る. 扱う入力は1つなので,平均と分散を求めることができないのでどうするか.
この問題を解決するために,学習時に計算した平均と分散を使う.
学習時には,各バッチごとに各レイヤーの平均と分散が得られる. この各レイヤーごとの平均と分散から指数移動平均を求めてとっておき,それを予測時の平均と分散として用いることでこの問題を解決することができる.
Multi-class classification
これまでは,binaryClassificationの例を見てきた. ここからは多クラス分類について見ていく.
Softmax Regression
これまでは,「この画像は猫か?」というような問題を扱ってきた. ここからは「この画像は猫か犬かひよこかそれ以外か?」という問題を扱う.
上記の例は4つのクラスへの分類と表現できる. 正解ラベルが,猫であれば1,犬であれば2,ひよこであれば3,それ以外であれば0だとする.
これを分類するネットワークは図6のように表せる.
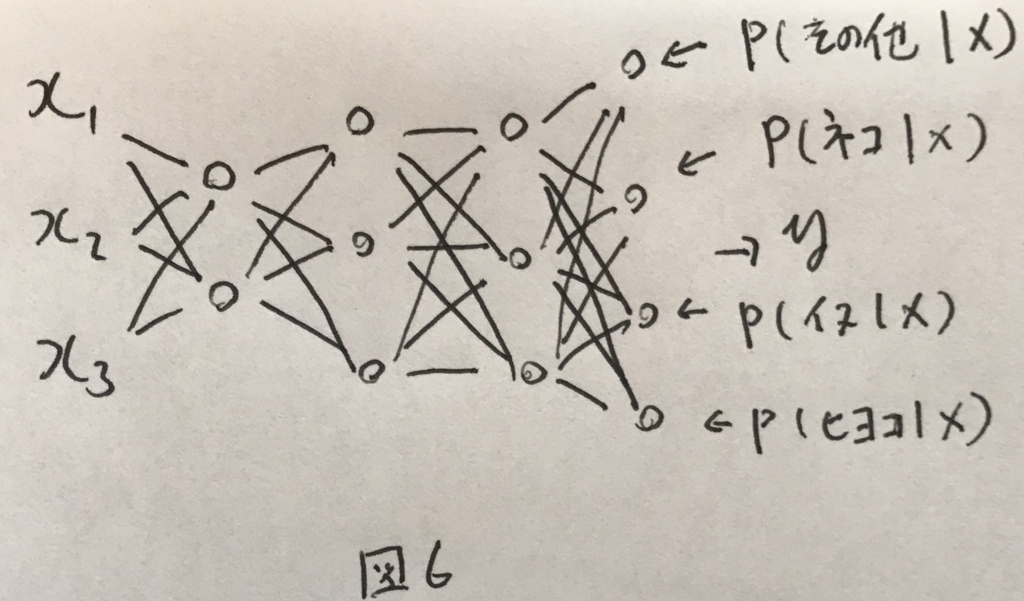
最終的な層がクラスの分になっている点がこれまでとの違いである. 最終的な層には,各クラスである確率を表現させたい. 例えば,0番目は入力がクラス0(つまりその他)である確率を表現させ,1番目には入力がクラス1(つまり猫)である確率を表現させる.
これを表現させるために最後の層の活性化関数としてよく用いられるのがsoftmax関数である. softmax関数は図7の式で表せる.全てのクラスについて確率を足し合わせると1になる特徴を持つ.
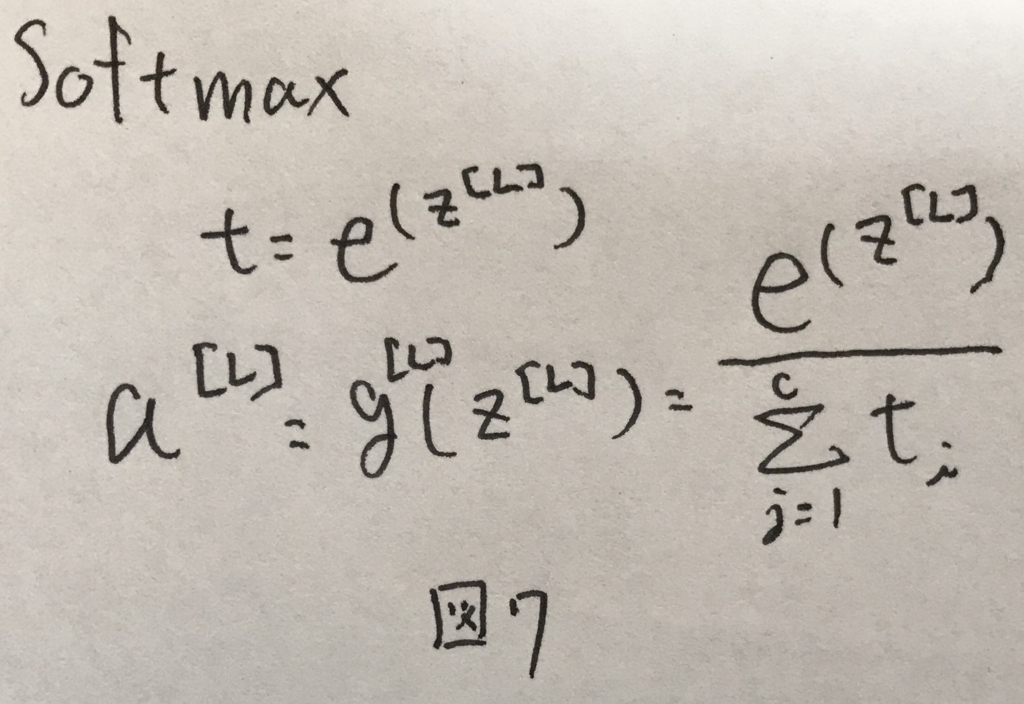
Training a softmax classifier
多クラスの場合のネットワークの学習について. 損失関数とコスト関数は図8のように表せる.
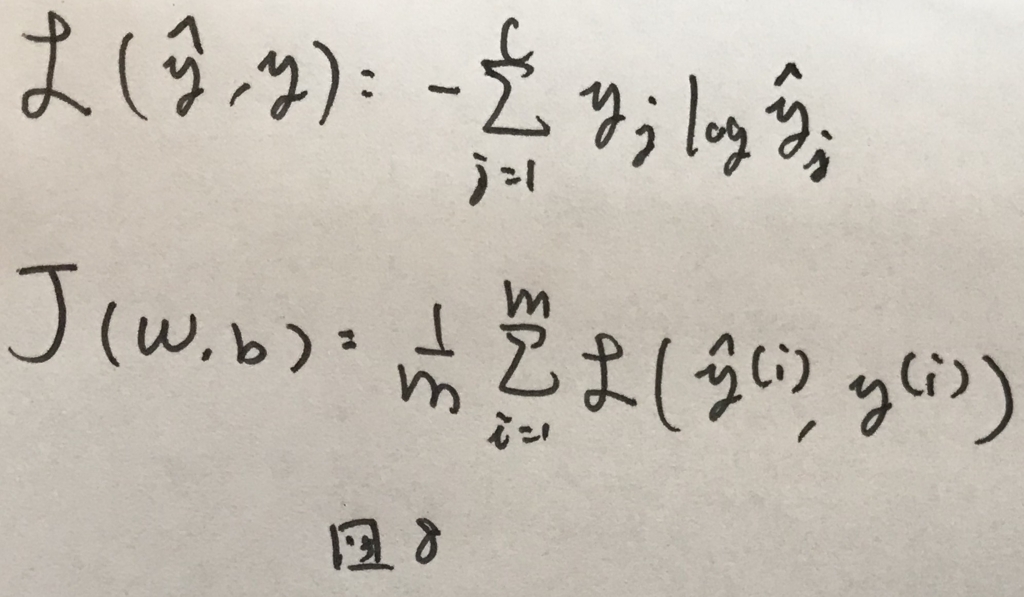
このコスト関数において,誤差逆伝播の際に使われる一番はじめの誤差は図9のように求まる.
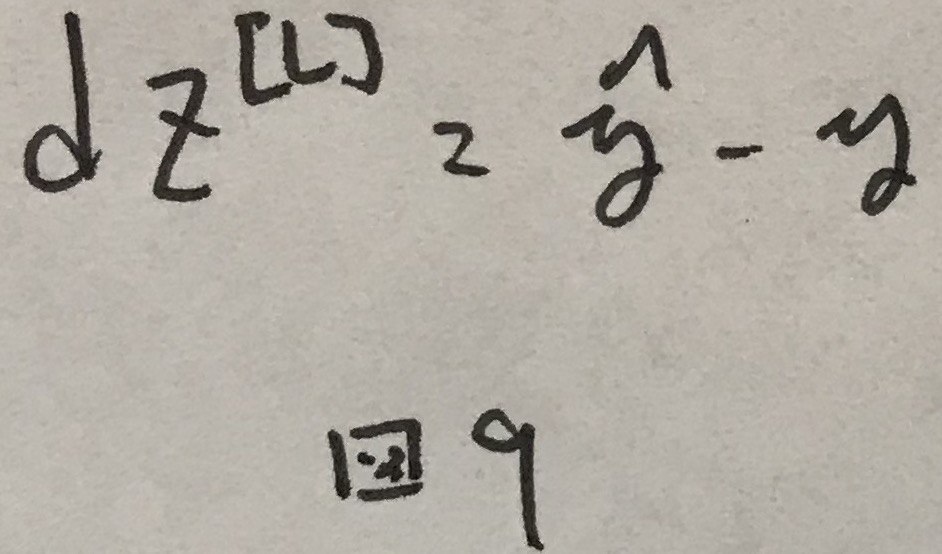
あとはいつも通り学習を進めれば良い.
Introduction to programming frameworks
DeepLearningのためのフレームワークの説明. 割愛.
Optimization algorithms
CouseraのDeepLearningコースの学習メモ続きです.
Mini-batch gradient descent
MachineLearningのプロジェクトは反復的にモデルを育てていくような進め方になるので,早く学習を進めることができる仕組みはとても大切になる.
これまで見てきた最急勾配法は明示的なfor文を取り払い,素早く学習が進むようにベクトル化して最適化が効きやすいようにしていた.
とはいえ,サンプル数が大きいと,やはり時間がかかってしまう.
全てのデータを学習の1step毎に使うのはサンプル数の増大に合わせてかかる時間が大きくなりすぎる.
これを解決するために,一度に全てのデータを使う方法ではなく,小さい単位に分けて,ちょっとずつ使っていくような方法がある.小さい単位のことをミニバッチ(mini-batch)とよび,これを活用して勾配法を行うものをミニバッチ勾配法と呼ぶ.なお,これまで通り一度に全てのデータを活用する方はバッチ(batch)と呼ぶ.
50000件データが存在している場合に1000データずつ分けたイメージを図1に示す.

なお,ミニバッチのインデックスを表す変数としてはtを使う.
ミニバッチを用いた勾配法のアルゴリズムを図2に示す.

図2の中で,for文がt=1toTまで繰り返されると,全てのデータについての1回の学習が完了する.全てのデータについての1回の学習を行うことを1epochと呼ぶ.
Understanding mini-batch gradient descent
コスト関数の特徴について
全てのデータを毎回使う方法であれば,コスト関数は単調減少するが,ミニバッチ法は毎回ミニバッチに対してのみ処理を行うため,コスト関数は単調減少しない. トレンド的には下がるが,毎回必ず下がるわけではなく,図3のような違いが出てくるという特徴がある.

ミニバッチサイズの決め方について
ミニバッチのサイズがデータ総量と等しいように設定すると,それはバッチで行う最急勾配法と同義になる. ミニバッチのサイズを1とすると,全てのデータが独立してミニバッチになり,学習1step毎に1つのデータのみを扱うことになる.これを確率的勾配法と呼ぶ.
最急勾配法は全てのデータを1stepに使うので当然時間がかかるという問題がある. 一方で,確率的勾配法であれば1stepに1データしか使わないので,一見すると早そうだが,この状態ではベクトル化の恩恵を得ることができず,逆に時間がかかるといった問題を引き起こす.
なので,ミニバッチサイズは大きすぎず,小さすぎず,いい感じに調整する必要がある. いい感じにミニバッチサイズを決めるためのガイドラインとしては,以下の通り.
- 小さいデータ量(m<2000程度)であればバッチで行う
- それ以上であれば,64,128,256,512くらいのサイズから選択する
64,128,256,512はそれぞれ2の累乗であり,計算機で扱う上で最適化が行われ計算速度が上がる可能性があるため,この値を選んでいる. なお,処理するコンピュータの性能と相談しながら,1度に使いたいデータがメモリ上で処理できることも重要な要素となる.メモリ上で保持できない場合はI/Oが走るため,処理が遅くなるためである.
Exponentially weighted averages
勾配法による学習自体を効率化するための方法を以下数章で説明する.
まず,この章では,そのための基礎となるExonentially weighted averages(指数加重移動平均)という考え方の説明を行う.
指数加重移動平均は図5の式で与えられる.

この式の意味について考えるために,例としてとある地域の気温グラフ(図4)を考える.

このグラフに対して指数加重移動平均をとると,図4'のように平均気温の推移が得られる.

Understaning exponentially weighted averages
t=100の場合を考えると,図6に示すように,過去のデータを減衰させながら少しずつ取り入れるような仕組みになっている.

このように.指数加重移動平均は過去のデータの寄与を取り入れて値の推移を滑らかに表すことができる指標と言える.
なお,指数加重移動平均の最初の方は著しくデータが小さい値になるという問題がある. v0=0として初期化しているので,ある程度tが進むまでは「これまでの値」が存在しないためである. これをいい感じに補正するためにBiasCorrectionという処理を行う. これは単純に,指数加重移動平均の値に図7に示す式を掛け算して補正してあげることを示す.

Gradient descent with momentum
指数加重移動平均を使って,普通の勾配法より早く学習が進む方法,Momentumを紹介する. 通常の勾配法では,パラメータの更新にコスト関数の微分した結果をそのまま用いていたが,これを指数加重移動平均に置き換える.つまり図8のようなアルゴリズムになる.

こうすると学習が図9のようになる.勾配の平均が更新に大きく関わってくるので,常に存在する水平方向への学習は加速され,常に符号が反転する垂直方向への学習は行われなくなるのである.

これによって,学習効率が上がる.
RMSprop
Momentumと似たようなもので,RootMeanSquareProp(RMSprop)という方法もある. アルゴリズムを図10に示す.

この方法によっても,学習の効率をあげることができる.
Adam optimization algorithm
MomentumとRMSpropを組み合わせた方法をAdam(Adaptive moment estimation)と呼ぶ. アルゴリズムを図11に示す.

Adamのhyperparameterを図12にまとめる. このうち,αは実装者によるチューニングが大切になるが,他の値はだいたいデフォルトの値を使っておけば間違いはない.

Learning rate decay
学習の最初の方では学習率を大きく設定することで,学習スピードを高め,学習がある程度進んだら学習率を小さくしてちょっとずつ進みたいと言ったようなこともできる.
学習率に,学習回数をパラメータとした値を掛け算してあげるような式であればこれが実現できる. いくつか種類があるようだ.
The problem of local optima
最適化を進めるなかで,コスト関数が鞍状だった際に学習スピードが遅くなるという問題がこれまであったが,Adamのように,移動平均を用いて同一方向への学習が加速していくような仕組みを採用するとその問題は気にしなくて良くなるので便利というお話.
Practical aspects of Deep Learning
CorseraのDeepLearningのコースの学習メモです.
今回はニューラルネットワークを効率的に学習させるための知識を学ぶ.
Train/Dev/Test sets
ニューラルネットワークには様々なHyperParameterが存在する. 実際に各パラメータを試さずして,最適なものを見つける方法は現時点ではなく,効果的に調整することが求められる. この調整では,ネットワークの学習を行い,それを用いて動作確認してみてモデルの性能を確認し,満足するまでパラメータのチューニングを行う.
効果的にこれを実践するために,手元に得られているデータを3つの役割で分けて使い分けることがオススメ.分ける3つはトレーニングセットとデベロップメントセット,そしてテストセットである.
トレーニングセットはその名の通り,モデルの学習時に用いられるデータ群である. デベロップメントセットは,学習済みモデルの性能を確認し,パラメータの調整を行うために用いられる. さらに,テストセットはチューニングが完了した後に,最終的なモデルの性能を確認するために用いられるデータセットである.
基本的にそれぞれの役割にデータは一意に割り当てられ,被らないようにする.
全てのデータをトレーニングセットとして扱い,そのモデルの精度の評価にそこからデータを取り出して用いるような使い方では,過学習の問題を検知することができないので,アプリケーションとして提供する際に所望の性能が得られないからである.
データの割合は,総数が100-10000くらいのレンジであればTrain(60%)/Dev(20%)/Test(20%)くらいの分量に分ける.
さらに総量が増えて1000000くらいの量になって来た場合は,そこまでたくさんのDevセットやTestセットは不要なので,例えばTrain(98%)/dev(1%)/Test(1%)といったようなデータの扱い方でも問題はない.
Bias/Variance
バイアスとバリアンスについて. 学習済みモデルの性能を評価する指標として,バイアスとバリアンスがある.
図1にバイアスが高い状態とバリアンスが高い状態のそれぞれのイメージを示す.

これは2変数のモデルの分類問題で,決定境界がそれぞれ示されている.
バイアスが高い状態のものは決定境界が線形であり,十分に高い精度の決定境界が得られていない. 一方で,バリアンスが高い状態のものは,決定境界が過剰に複雑になっており,トレーニングサンプルについては高い精度での分類ができているように見える. ただ,未知のデータを分類しようとした場合に,過剰にトレーニングサンプルに適応されており,適切な分類が行えないという問題がある.これはトレーニングサンプルが少なかったり,無駄にモデルが複雑な場合に発生する問題である.
高いバイアスは「トレーニングサンプルについて正しく決定境界が得られていない」状態を,高いバリアンスは「トレーニングサンプルについては満足できる決定境界が得られているものの,未知のデータについては正しくない」状態をそれぞれ指す.
テストセットに対する判定精度とデベロップメントセットに対する判定精度を比較することで,いまモデルがどんな状態にあるのかを図2のように判定することができる.

Basic Recipe for Machine Learning
バイアスが大きいか,バリアンスが大きいかによって,モデルをより良い精度で動かすためにするべきことが異なる. ここでは,それぞれのケースですべき,基本的な事項を図3にまとめる.

なので,例えばバイアスが高い状態では,いくらデータを増やしても問題解決には直結しないので注意が必要.
Regularization
ここでは正則化について説明する. 正則化はバリアンスが高い時に試すべき方法の一つで,バイアスを上げてしまうデメリットはあるが,データ採取などのコストをかけずにバリアンスを下げることが狙える手法である.
バリアンスが高い=過剰にくねくねした決定境界になっているという状態であり,これはモデル(W)のそれぞれの値が大きくなりすぎている時に起きる. なので,Wの値が大きくなりすぎないようにすることで,バリアンスを下げることが可能になる.
Wの値が大きくなりすぎないようにするために,ニューラルネットワークの学習時に最小化したいコスト関数に,Wができるだけ小さくなるような項を含めることで,これを実現する.この,できるだけ小さくなるような項はいろんな選択肢があり,図4に示すような場合をL2正則化と呼ぶ.

このコスト関数を使った際の更新式は図5に示す通りになる. なお,λという値が初めて出て来た. これは正則化の程度を表す値であり,実装者によって調整されるべきHyperParameterの1つである.

なお,αもλもmも正の値であるため,(1-αλ/m)は1よりわずかに小さい値になるので,この式の意味としては「学習ごとにWを少しだけ小さい値に減衰させていく」ことを意味する.
この直腸からL2正則化は重み減衰とも呼ばれる.
Why regularization reduces overfitting?
では,何故これによってoverfittingが起こらなくなるのかを,感覚的に説明する. なお,overfittingとは高いバリアンスを引き起こすようなトレーニングデータに対する過剰適応のことである.
λを大きくすればするほど,コストに占めるWの大きさの割合が増えるため,Wが小さくなることに対する興味が大きくなる.すると各Wの値は0に近づき,結果としてモデルがより単純な形になるため,overfittingを防ぐことができる.
Dropout Regularization
L2正則化の他にも正則化のテクニックがある. ドロップアウトはその中でも代表的な方法であり,L2正則化と同様によく使われる.
学習時に確率的に各レイヤーのノードを無効化して学習を進めるといった方法で,これを行うことで正則化効果を得ることができる.
Understanding Dropout
ドロップアウトを行うと,学習毎にノードの一部が消滅している状態になるので,学習するモデルが全てのノードをそのまま使う時に比べて小さくなる.その結果,overfittingを防ぐことが可能になる. また,確率的に全てのノードが不通になるので,1つの特徴に強く依存したモデルが作られにくい.1つの特徴に強く依存しているような場合は,特定のWの値が大きくなるが,ドロップアウトによってこれを防ぐことができる.つまりL2正則化と似たような効果が得られるわけである.
Other regularization methods
正則化の方法として他にも,既存のデータを工夫して増やすデータ拡張や学習の早期終了などがある.
Normalizing inputs
この章では,学習効率をあげるための,入力の正規化についてのべる. これを行うことで学習スピードを早めることができる.
簡単に説明すると,図6aのような入力を,図6bのような形に変えてあげることで学習を早めようというテクニックである.

これを入力に対して行うことで,学習が最適化されやすくなり,学習効率が高まる.
正規化の手順を以下に示す. まず,それぞれの特徴x1,x2について平均μを求める. 次に,各特徴の分散σを求める.
上記の平均と分散を用いて各特徴を図7の式の通り正規化する.

これで図6bのような平均が0で分散が1の特徴量空間への写像が完了する.
なお,トレーニング時に用いたμとσは取っておいて,予測時にも入力データに対して同様の前処理をかけるようにしなくてはいけないので注意が必要.
Vanising/Exploding gradients
深いネットワークの学習において,勾配爆発/消失の問題がある. これが発生するとモデルの学習が行われなくなる. これの発生原理の説明を行う.
簡単のために,図8のようなネットワークを考える. また,活性化関数が線形写像(g(z)=z)として考える.

この時y^は図9のように表せる.

ここで,Wを図10のように初期化するとy^の値が指数関数的に増大もしくは減少する.

これが勾配爆発/消失の問題である.
Weight Initialization for Deep Networks
上記を完全ではないが,ある程度防ぐことのできる,Wの初期化方法がある. 初期化方法は使う活性化関数によって異なるが,偏差が特定の値になるように調整することで実現される. 図11に活性化関数毎の初期化値を示す.

Gradient checking
勾配法を実装する際に,デバッグで活用できるGradientCheckingについての解説.割愛.
Gradient Checking Implementation Notes
GradientCheckingを実装する上での注意点を解説している.割愛.